
第二节方差(Variance) 一、方差的定义 二、方差的性质 三、常见分布的方差 四、契比雪夫不等式
一、方差的定义 二、方差的性质 三、常见分布的方差 四、契比雪夫不等式 第二节 方差 (Variance )
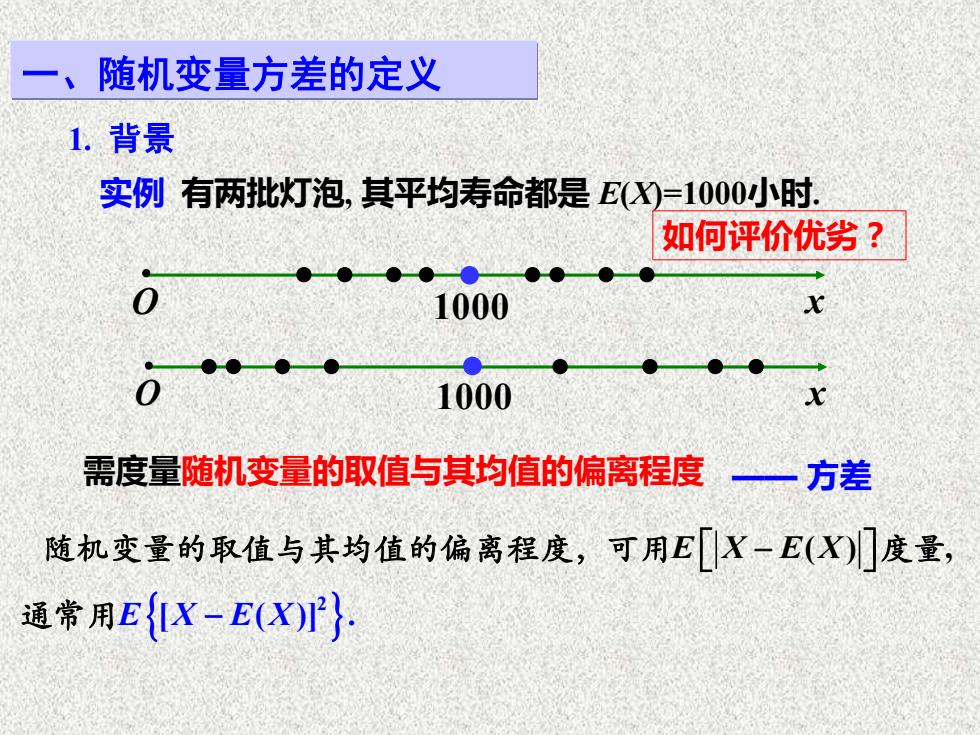
一、随机变量方差的定义 1.背景 实例有两批灯泡,其平均寿命都是E()=1000小时. 如何评价优劣? 0 1000 x ● 1000 需度量随机变量的取值与其均值的偏离程度一—方差 随机变量的取值与其均值的偏离程度,可用E[X-E(X)川度量, 通常用E{K-E(X}
1. 背景 实例 有两批灯泡, 其平均寿命都是 E(X)=1000小时. • O x • • • • • • • • • O x • • • • • • • • • 1000 • 1000 一、随机变量方差的定义 如何评价优劣? 需度量随机变量的取值与其均值的偏离程度 —— 方差 E X E X − ( ) , 随机变量的取值与其均值的偏离程度,可用 度量 2 通常用E X E X [ ( )] . −

2.定义设X是一个随机变量,若E{LX-E(X)}存在,则称 ELX-E(X)}为X的方差,记为D(X)或Var(X),即 D(X)=Var(X)-Ex-E(X Variance 称√D(X)为标准差或均方差,记为σ(X). 注:方差刻划了随机变量的取值对于其数学期望的偏离程度。 方差一就是随机变量X的函数g(X)=[X-E(x)]的数学期望!
2. 定义 2 2 , {[ ( )] } , {[ ( ) ] } ( ) Var( ), X E X E X E X E X X D X X − − 方 设 是一个随机变量 若 存在 则称 为 的 差,记为 或 即 注:方差刻划了随机变量的取值对于其数学期望的偏离程度。 称 D( ) , X 为标准差或均方差 记为σ( ). X 2 D X X E X E X ( ) Var( ) ( ) . = = − 2 方差——就是随机变量X g X X E x 的函数 ( ) ( ) = − 的数学期望! ( Variance )

定理1°设X为离散型随机变量,分布律为 P{X=x}=p(k=1,2,),若∑x-E(X)P k=1 绝对收敛,则D=2x-E(Xn. 2°设X为连续型随机变量,概率密度为f), 若∫Ix-E(X)f(x)dx绝对收敛,则 DX=∫Ix-E(X)Ff(x)dx
定理 1 o 设 X 为离散型随机变量,分布律为 { } ( 1,2, ) P X x p k = = = k k ,若 2 1 [ ( )] k k k x E X p = − 绝对收敛,则 2 1 ( ) [ ( )] k k k D X x E X p = = − 。 2o 设 X 为连续型随机变量,概率密度为 f (x), 若 2 [ ( )] ( )d x E X f x x − − 绝对收敛,则 2 D X x E X f x x ( ) [ ( )] ( )d − = −
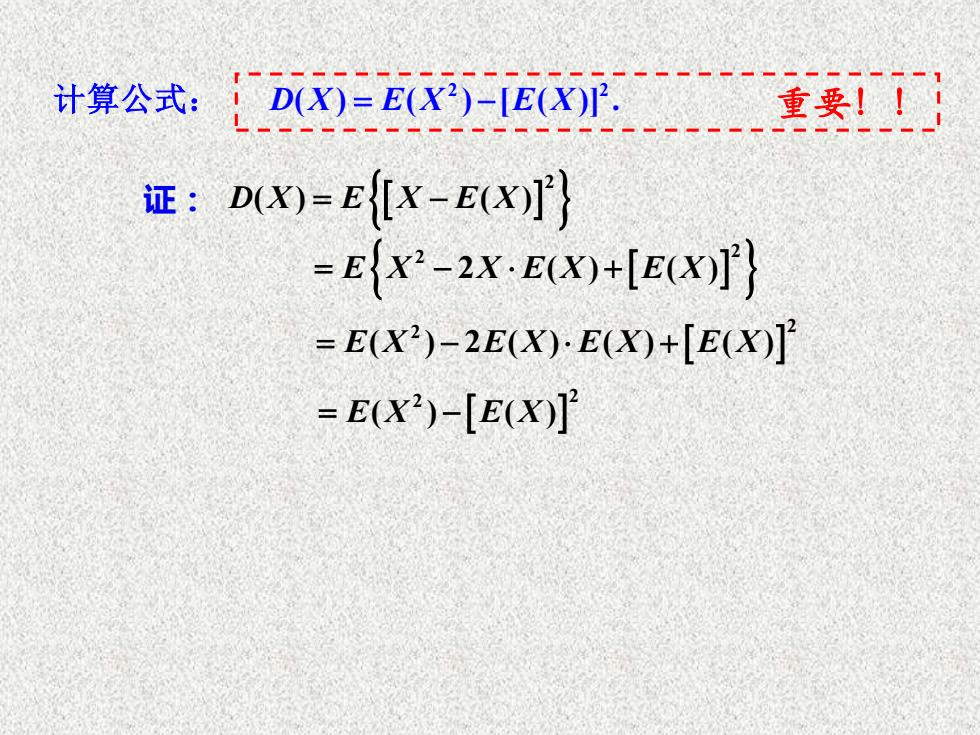
计算公式: D0=E)-EP重!1 证:DX=Ex-E(X'} =E{x2-2X.E(X)+[E(X)]} =E(X)-2E(X)·E(X)+[E(X)] =E(X2)-[E(X)]
计算公式: 2 D X E X E X ( ) ( ) = − 2 2 = − + E X X E X E X 2 ( ) ( ) 2 2 = − + E X E X E X E X ( ) 2 ( ) ( ) ( ) 2 2 = − E X E X ( ) ( ) 证: D X E X E X ( ) ( ) [ ( )] . = − 2 2 重要!!