
复习:一维连续型随机变量的函数的分布 问题:已知X的密度fx(x),求Y=g(X)的密度f(Oy) 方法1 F,(y)=P{Y≤}=P{g(X)≤y} =∫sfx(dx,(-o<x<o,F0I=f少 方法2 o-g8 其它 y=g(x)处处可导,且恒有g'(x)>0(<0), x=(Uy)是g(x)的反函数,a<y<B(是y=g(x)的有效值域) (a,)=)且1田≠0)-
复习:一维连续型随机变量的函数的分布 ( ) { } { ( ) } F y P Y y P g X y Y = = ( ) ( )d , ( ), X g x y f x x x = − 方法1 方法2 [ ( )] ( ) , , ( ) 0, . X Y f h y h y y f y = 其它 ( ) ( ) ( ) 问题:已知X f x Y g X f y 的密度 X Y ,求 = 的密度 [ ( ) ] ( ) F y f y Y y Y = ( ) ( ) 0( 0), ( ) ( ) , ( ( ) ) y g x g x x h y g x y y g x = = = 处处可导,且恒有 是 的反函数 是 的有效值域 ( , ( ) ( ) 0 )= y y g x f x = 且

第五节 两个随机变量函数的分布 (一)Z=X+Y的分布 (-yZ=及Z=X灯的分布 X (三)M=max(X,Y)及N=min(X,Y)的分布
第五节 两个随机变量函数的分布 Y Z Z XY X = = (二)* 及 的分布 (一)Z X Y = + 的分布 (三)M X Y N X Y = = max( , ) min( , ) 及 的分布
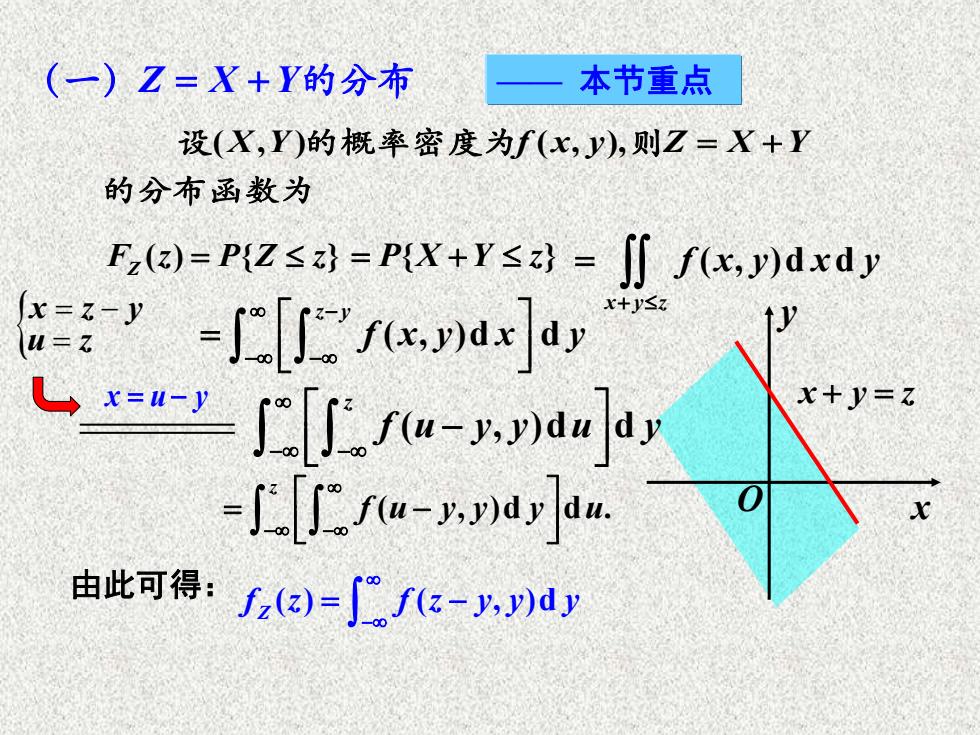
(一)Z=X+Y的分布 本节重点 设(X,Y)的概率密度为f(x,y),则Z=X+Y 的分布函数为 Fza)=P{Z≤=PX+r≤z=∬fx,y)dxdy &’-[xa x+y≤ Le-g∫[a-a]ay Ax+y=z =∫[fu-ar小a 由此可得:fa)=∫fz-y,dy
设( , ) ( , ), X Y f x y Z X Y 的概率密度为 则 = + 的分布函数为 ( , )d d x y z f x y x y + = x y O x y z + = ( , )d d z y f x y x y − − − = x u y = − ( , )d d z f u y y u y − − − 由此可得: (一)Z X Y = + 的分布 —— 本节重点 ( ) { } F z P Z z Z = = + P X Y z { } x z y u z = − = ( , )d d . z f u y y y u − − = − f z f z y y y Z ( ) ( , )d − = −

za)=∫mfz-y)dy 同理可得:z2)=fx,z-x)dx XY独立时,f2a)=∫人(a-O)dy fa)=J」f(x)f(&-x)dx 这两个公式称为∫x和f,的卷积公式,记为x*,即: f*f=J」人xa-yf)dy=∫」fx(xf,-dx 5:e=f(,)dxdy主了f.(f(ydxdy x+y≤z x+y≤2
X, Y 独立时, f f f z y f y y X Y X Y * ( ) ( )d − = − ( ) ( )d . X Y f x f z x x − = − f z f x z x x Z ( ) ( , )d − = − f z f z y y y Z ( ) ( , )d − = − f z f z y f y y Z X Y ( ) ( ) ( )d − = − f z f x f z x x Z X Y ( ) ( ) ( )d − = − 同理可得: 这两个公式称为 X Y f f X Y 和 的 卷积公式, 记为 f f ,即: ( , )d d x y z f x y x y + ( ) F z Z = X Y, 独立 X Y ( ) ( )d d x y z f x f y x y +

例1.设两个独立的随机变量X与Y都服从标准正态分布, 求Z=X+Y的概率密度。 解:因f田=1e号 =e2,-0<x<0 f0-2 e 2,-oo<p<00, 阳-f-ar-0e,号a: 2π 1e, =√π 即Z服从N(0,2)分布。 2√π
1. X Y Z X Y = + 例 设两个独立的随机变量 与 都服从标准正态分布, 求 的概率密度。 解: 因 2 2 1 ( ) , 2 x X f x e x − = − 2 2 1 ( ) , , 2 y Y f y e y − = − 2 z 2 2 t x = − 1 4 2 d 2 z z x e e x − − − − = 2 2 4 1 d 2 z t e e t − − − 2 4 1 , 2 z e − = f z f x f z x x Z X Y ( ) ( ) ( )d − = − 2 2 ( ) 2 2 1 d 2 x z x e e x − − − − = 即Z N 服从 (0 2,)分布。 =