
第四节连续型随机变量及其概率密度 一、连续型随机变量及其 概率密度的概念与性质 二、常见连续型分布
一、连续型随机变量及其 概率密度的概念与性质 二、常见连续型分布 第四节 连续型随机变量及其概率密度

一、连续型随机变量及其概率密度 1.定义 如果对于随机变量X的分布函数F(x),存在非负函数f(x), 使对于任意实数x有Fx)=」nfu)d, 则称X为连续型随机变量,其中(x)称为X的概率密度函数, 简称概率密度 注:连续型随机变量X的分布函数F(x)是连续函数
一、连续型随机变量及其概率密度 1. 定义 ( ) ( ) ( ( )d , ) x X f x F x f F x x t t − = 如果对于随机变量 的分布函数 ,存在 , 使对于任意实数 有 非负函数 , ( ) . 则称 X f 为连续型随机变量 其中 x 称为 X的概率密度 , 简称概 数 率密度 函 注:连续型随机变量X的分布函数F x( ) . 是连续函数

2.性质 F)=P{X≤x=∫f)di (1)f(x)20; (2)∫nfx)dx=1 (3)对于任意实数x1,x2(x1≤x2) P(x<X5x)=F(x2)-F(x)=["f(x)dx. f)1 同时得以下计算公式 P{X≤d=Fa-∫nfw)dx P{X>a}=1-PX≤ =1-Fa)=∫fx)dx. (4)若f(x)在点x处连续,则有F(x)=f(x):
(1) ( ) 0; f x (2) ( )d 1 f x x − = 1 2 1 2 (3) , ( ) 对于任意实数 x x x x 2. 性质 ( ) ( )d x F x P X x f t t − = = P X a F a { } ( ) = ( )d , a f x x − = P X a P X a { } 1 { } = − = −1 ( ) F a ( )d . a f x x = 同时得以下计算公式 o x f x( ) 1 x • 2 x • (4) ( ) , 若 f x x 在点 处连续 则有 F x f x ( ) ( ). = 1 2 P x X x { } 2 1 2 1 ( ) ( ) ( )d . x x = − = F x F x f x x

例1.设随机变量X具有概率密度 kx, 0≤x<3, f2- 3≤x≤4, 典型题型! 0, 其他. (1)确定常数k; O求X药分布画我:⊙)米Pl<Xs 解(④由∫f(x)dx=1, 得心cdx+2-dx=l解之得k=
, 0 3, ( ) 2 , 3 4, 2 0, . 7 (1) ; (2) ; (3) {1 . 1 } 2 . X kx x x f x x k X P X = − 设随机变量 具有概率密度 其他 确定常数 求 的分布函数 求 例 解 (1) ( )d 1, f x x − = 由 3 4 0 3 d (2 )d 1, 2 x kx x x + − = 得 1 . 6 解之得 k = 典型题型!
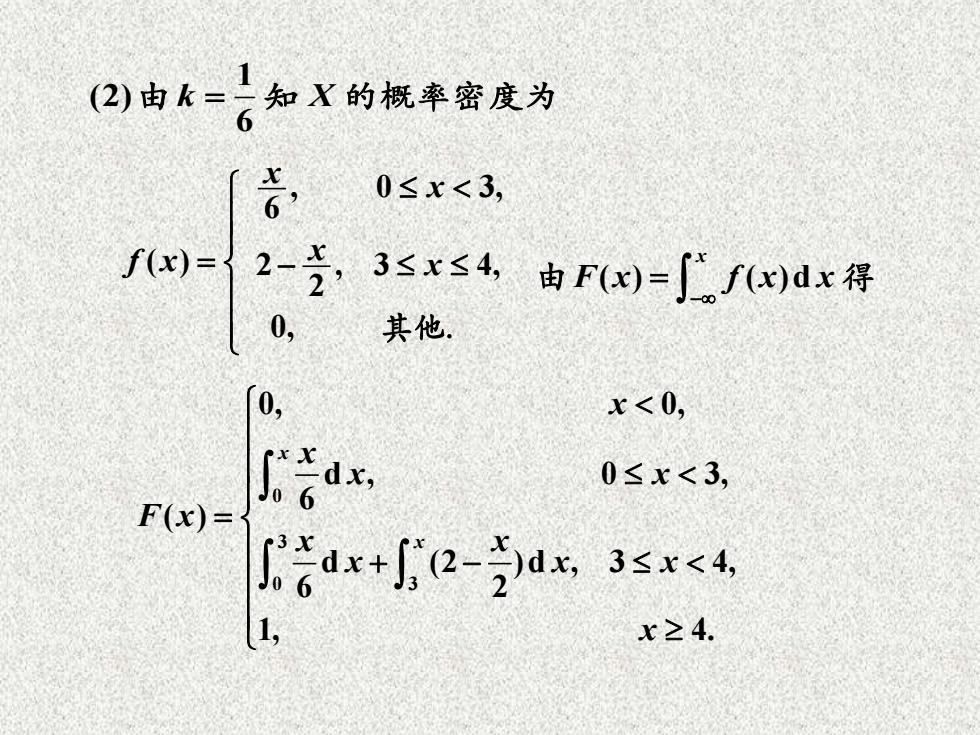
(2)由k=二知X的概率密度为 6 若 0≤x<3, f(x)= 2-克3sx≤4,由F=∫广fdx符 0, 其他 0, x<0, ax 0≤x<3, F(x)= 若dr+2-x,3≤x<4 1, x≥4
f x( ) = , 0 3, 6 2 , 3 4, 2 0, x x x x − 其他. 1 (2) 6 由 k X = 知 的概率密度为 ( ) ( )d x F x f x x − = 由 得 0 3 0 3 0, 0, d , 0 3, 6 ( ) d (2 )d , 3 4, 6 2 1, 4. x x x x x x F x x x x x x x = + −