(2)若p>1,因为当n-1≤xsn时,1≤1 ,故 i] [小女 4-o n-→ 故该级数收敛,由比较审敛法知p级数收敛
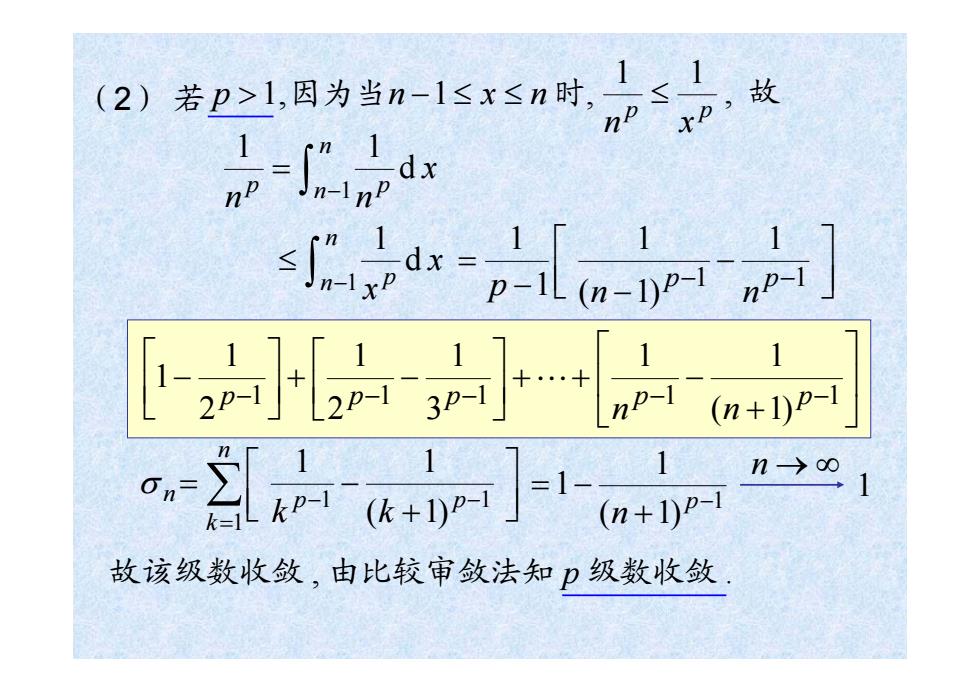
p > 1,因为当 n − 1 ≤ x ≤ n , 1 1 p p n x ≤ 故 ∫ − = n p n p x n n 1 d 1 1 ∫ − ≤ n n p x x 1 d 1 ⎥⎦ ⎤ − − ⎢⎣ ⎡ − = − 1 − 1 1 ( 1 ) 1 1 1 p p p n n 考虑级数 ⎥⎦ ⎤ − − ⎢⎣ ⎡ − − ∞ = ∑ 1 1 2 1 ( 1 ) 1 p p n n n 的部分和 σ n ⎥⎦ ⎤ + − ⎢⎣ ⎡ = − − = ∑ 1 1 1 ( 1 ) 1 1 p p n k k k n → ∞ 故该级数收敛 , 由比较审敛法知 p 级数收敛 . 时, 1 ( 1 ) 1 1 − + = − p n ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − 1 − 1 − 1 − 1 − 1 ( 1 ) 1 1 3 1 2 1 2 1 1 p p p p p n n " 1 ( 2 ) 若

p级数2山 n=i np 当p>1时收敛,当p≤1时发散 调和级数与p级数是两个常用的比较级数。 练习若存在N∈Z,对一切n≥N, 、10 ()un≥,则∑4n 发散 n n=1 2少期 收敛 n-1
调和级数与 p 级数是两个常用的比较级数. 若存在 , + N ∈Z 对一切n ≥ N , , 1 (1) n un ≥ ( 1), 1 (2) ≤ p > n un p p−级数 p n n 1 1 ∑ ∞ = : 当 p>1 时收敛,当p ≤1时发散. 练习 1 则∑ ∞ n= un 1 则∑ ∞ n= un 发散 收敛

1 例2证明级数 白√nn+ 发散 证因为 m-4o-12 而级数 发散 根据比较审敛法可知,所给级数发散
证明级数 ∑ ∞ = + 1 ( 1) 1 n n n 发散 . 证 因为 2 ( 1) 1 ( 1) 1 + ≥ n n + n ( 1, 2, ) 1 1 = " + = n n 而级数 ∑ ∞ = + 1 1 1 n n ∑ ∞ = = 2 1 k k 发散 根据比较审敛法可知, 所给级数发散 . 例2