
矩阵范数 ·矩阵范数定义 ·设km×n表示数域k上全体m×n阶矩阵的集合 ·若对于km×n中任一矩阵A,均对应一个实值函数, 并满足以下条件 -非负性:A≥0,等号当且仅当A=0时成立; -齐次性:laA=alA,a∈k; - 三角不等式:A+B≤A+B,A,B∈k ·则称A为广义矩阵范数,若还满足 相容性AB吲≤AIB ·则称剁A为矩阵范数 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 矩阵范数 矩阵范数定义 设km×n表示数域k上全体m×n阶矩阵的集合 • 若对于km×n中任一矩阵A,均对应一个实值函数, 并满足以下条件 – 非负性: ||A||≥0,等号当且仅当A=0时成立; – 齐次性: – 三角不等式: • 则称||A||为广义矩阵范数,若还满足 – 相容性 • 则称||A||为矩阵范数 A A , k; m n A B A B , A,B k AB A B
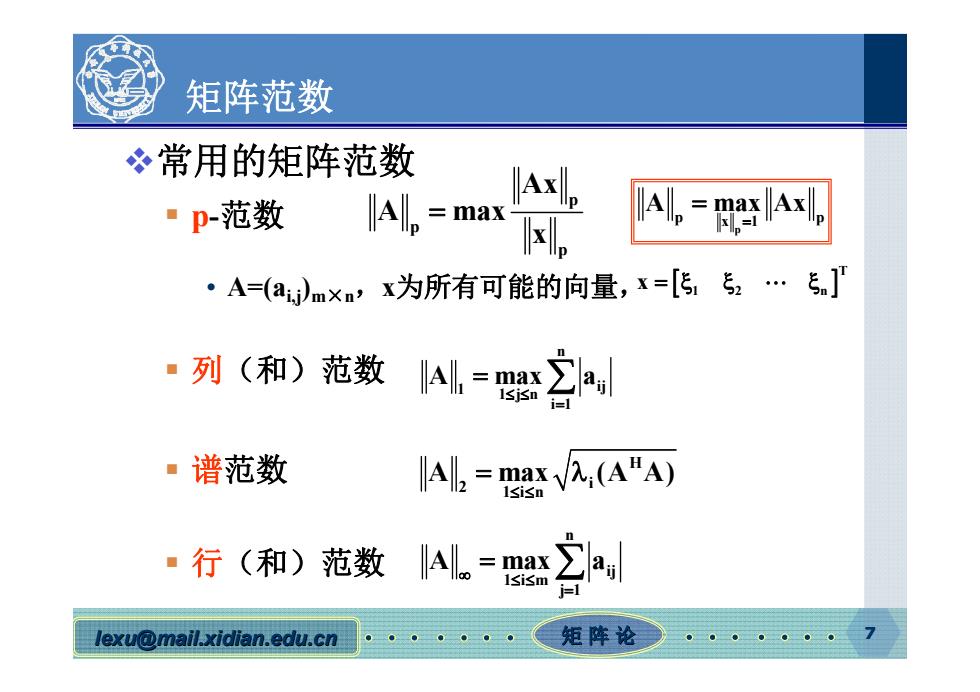
矩阵范数 冬常用的矩阵范数 lAxl, ·p-范数 max I可。 lAl-Axl x=1 ·A=(a)mxm,x为所有可能的向量,x=[5,5,…5.] ·列(和)范数 ·谱范数 A,=婴V(A"A) ·行(和)范数 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 矩阵范数 常用的矩阵范数 p-范数 • A=(ai,j)m×n,x为所有可能的向量, 列(和)范数 谱范数 行(和)范数 p p p Ax A max x T 12 n x p p p x 1 A max Ax n 1 ij 1jn i 1 A max a H 2 i 1in A max (A A) n ij 1im j 1 A max a

矩阵范数 ·F-范数robenis范数)A-(交, ·导出性范数 ·设x‖为数域k上n维向量空间km(k=R或C)的一种 向量范数。可定义矩阵范数为 - lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 矩阵范数 F-范数(Frobenius范数) 导出性范数 • 设||x||为数域k上n维向量空间kn(k=R或C)的一种 向量范数。可定义矩阵范数为 1 n 2 2 F ij i j1 A a , x 1 x0 Ax A max Ax max x

应用 必应用领域 ·逼近和误差估计是矩阵范数应用的主要领域 矩阵条件数cond(A)=AA‖ ·由相容性可知AA≥AA=I =xslx→回21 ·对于导出性范数川=1 cond(A)≥1 ·条件数反映了误差放大的程度,条件数越大, 矩阵越病态 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 应用 应用领域 逼近和误差估计是矩阵范数应用的主要领域 矩阵条件数 由相容性可知 对于导出性范数 条件数反映了误差放大的程度,条件数越大, 矩阵越病态 1 cond A A A 1 1 A A AA I x Ix I x I 1 I 1 cond A 1