
解:先证x(0)=0,在()中令s=t得,x(20=1c 2x(t) x(0)= 2x(0) 1-x2(0) →x(0)1+x2(0)=0→x(0)=0 其次,固定(1)中t(1)试两边关于s求导: xr+=X(s)1-x-x(s)+(0+xs)x0x's (1-x(t)x(s)月 x'(s)+x2()x's)_x'(s)(1+x2()) (2) (1-x(t)x(s)2 (1-x(t)x(s)乃 x'(t+S)= dx(t+s)d(t+s) d(t+s) 注意 d(t+s) ds d(t+s) 而 返回 结束
首页 上页 返回 下页 结束 铃 先证x s t (0) 0, (1) = = 在 中令 2 2 ( ) (2 ) 1 ( ) x t x t x t = − 得 2 2 (0) (0) 1 (0) x x x = − 2 x x x (0)(1 (0)) 0 (0) 0 + = = 其次,固定(1)中t s (1)试两边关于 求导: ( ) ( ) ( ) 2 ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) x s x t x s x t x s x t x s x t s x t x s − + + + = − ( ) ( ) ( ) 2 2 2 2 ( ) 1 ( ) ( ) ( ) ( ) (2) 1 ( ) ( ) 1 ( ) ( ) x s x t x s x s x t x t x s x t x s + + = = − − ( ) ( ) ( ) ( ) . ( ) ( ) dx t s d t s d t s x t s d t s ds d t s + + + + = = + + 解: 注意

S=0 则 (2)变为 0_x0)(1+x2) dt 00-ro(+ro)g (3)是一阶变量分离方程,求解得: arctanx(t)=x(0)t+c 由x(0)=0,得c=0.x(t)=tanx'(0)t 10.求一曲线,使它的切线介与坐标轴间的部分被 切点分成相等的部分: 解: 设所求曲线方程为y=Jx,M(x,y)为此曲线上任意 首页 上页 返回 下页 结束
首页 上页 返回 下页 结束 铃 ( ) ( ) ( ) 2 2 2 (0) 1 ( ) ( ) (0) 1 ( ) (3) 1 ( ) (0 dx t x x t x x t dt x t x + = = + − 令 s = 0 则 (2) 变 为 (3) arctan ( ) (0) 是一阶变量分离方程,求解得: x t x t c = + 由x c (0) 0, 0. = = 得 = x t x t ( ) tan (0) 设所求曲线方程为y yx M x y = , ( , )为此曲线上任意 10. 求 一 曲 线,使 它 的 切 线 介 与 坐标轴 间 的 部 分被 切 点 分成相 等 的 部 分. 解:
点.过M的切线与X轴及Y轴的交点 分别为A,B则A的坐标为 r兰,0的坐标为 M(x,y) (0,y-y)由题意 MA=MB因而我们 得到 P+2=V2+xy 首而 返回 结束 铃
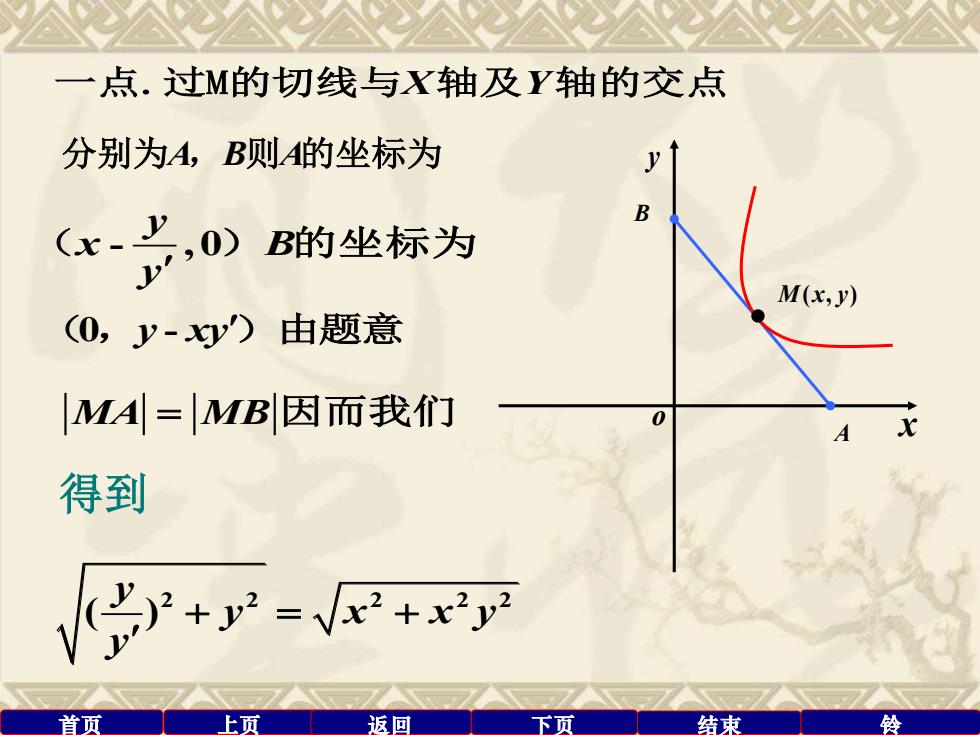
首页 上页 返回 下页 结束 铃 一点.过M的切线与X Y 轴及 轴的交点 分别为A B A , 则 的坐标为 - , 0 y x B y ( ) 的坐标为 (0 - ,y xy )由题意 MA MB = 因而我们 2 2 2 2 2 ( ) y y x x y y + = + 得到 y M x y ( , ) A B x o

而 +y2=x2+x2y2整理上试得: (y2+1D(y'+y)(y'-y)=0(*) 由(*)得:y'+y=0(1)或y'-y=0(不合题意舍去) 解1)得,y=c,其中c为任意常数. 习题(2.2) 10.求微分方程 =四+x+上 (a为常数)的通解. dx x 解: 1).设α=0,则此方程为一阶齐次线性方程,其通解为: 首页 上页 返回 下 结束
首页 上页 返回 下页 结束 铃 2 y 2 2 2 2 y x x y y +=+ 而 整 理 上 试 得: 2 (y xy y xy y + + = 1 ( )( - ) 0 (*) ) 由(*) 0 (1) - 0 得: xy y xy y + = = 或 (不合题意舍去) 解(1) , , 得 xy c c = 其中 为任意常数. 习题(2.2) 1 ( ) dy ay x a dx x x+ 10. 求微分方程 = + 为 常 数 的 通解. 解: 1 = . 0 设a ,则此方程为一阶齐次线性方程,其通解为:

y=∫t=x+n+c 2).设=1,此是方程为一阶非齐次线性方程,其通解为: y=e+*在+el='tc+d =x-I+m+cJ-xI+cx-1 3》.设a≠0,1此是方程的通解为: y=ej+e*+d小=r可f++d 结束
首页 上页 返回 下页 结束 铃 1 ln x y dx x x c x + = = + + 1 1 2 1 1 [ ] [ ] dx dx x x x x y e e dx c x dx c x x + + − = + = + 1 x x c x x cx [ ln ] ln 1 x = − + + = + −1 1 1 1 [ ] [ ( ) ] a a dx dx x x a a a x y e e dx c x dx c x x x − + + = + = + + 2 . 1, = 设a 此是方程为一阶非齐次线性方程,其通解为: 3 . 0,1 设a 此是方程的通解为: