
第四章线性方程组 二、非齐次线性方程组的通解 由性质4.3.1知,若已知(4-1)的一个解(特解)m*, 则(4-1)的任一解x总可以表示为 x=(x-n)+n=5+n (4-6) 其中5=x-1*为齐次方程组(4-5)的解 (4-6)式表明非齐次方程组(4-1)的任一解都可以表 示为它的一个特定解*与它的导出组一个解的和
第四章 线性方程组 二、非齐次线性方程组的通解 由性质4.3.1知,若已知(4-1)的一个解(特解)η* , 则(4-1)的任一解x总可以表示为 * * * x (x ) 其中ξ = x - η*为齐次方程组(4-5)的解. (4-6) (4-6)式表明非齐次方程组(4-1)的任一解都可以表 示为它的一个特定解η*与它的导出组一个解的和

第四章线性方程组 反过来,由性质4.3.2可知,对任何数k1,k2,kn-, x=k151+k252+.+km-,5m-r+7 总是方程(4-1)的解.因此 方程组(4-1)的通解为 x=k151+k252+.+km-,5m-,+7 其中51,52.,5n-,是(4-5)式的基础解系, k1,k2,km,为任意数
第四章 线性方程组 反过来,由性质4.3.2可知,对任何数 总是方程(4-1)的解. 因此 1 2 , , , n r k k k * 1 1 2 2 n r n r x k k k 1 2 , , , n r k k k * 1 1 2 2 n r n r x k k k 1 2 , , , n r 其中 是(4-5)式的基础解系, 为任意数. 方程组(4-1)的通解为

第四章线性方程组 例1求解方程组 1+X2-3x3-4=1, 3x1-x2-3x3+4x4=4, x1+5x2-9x3-8x4=0. 解对增广矩阵进行初等行变换化成行最简形 Γ11-3-11-3r「113-1 1 A=3-1-3 44 0-4 6 71 15-9803-1046 -7-1
第四章 线性方程组 1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x 例1 求解方程组 1 1 3 1 1 3 1 3 4 4 1 5 9 8 0 A 2 1 3 1 3 1 1 3 1 1 ~ 0 4 6 7 1 0 4 6 7 1 r r r r 解 对增广矩阵进行初等行变换化成行最简形
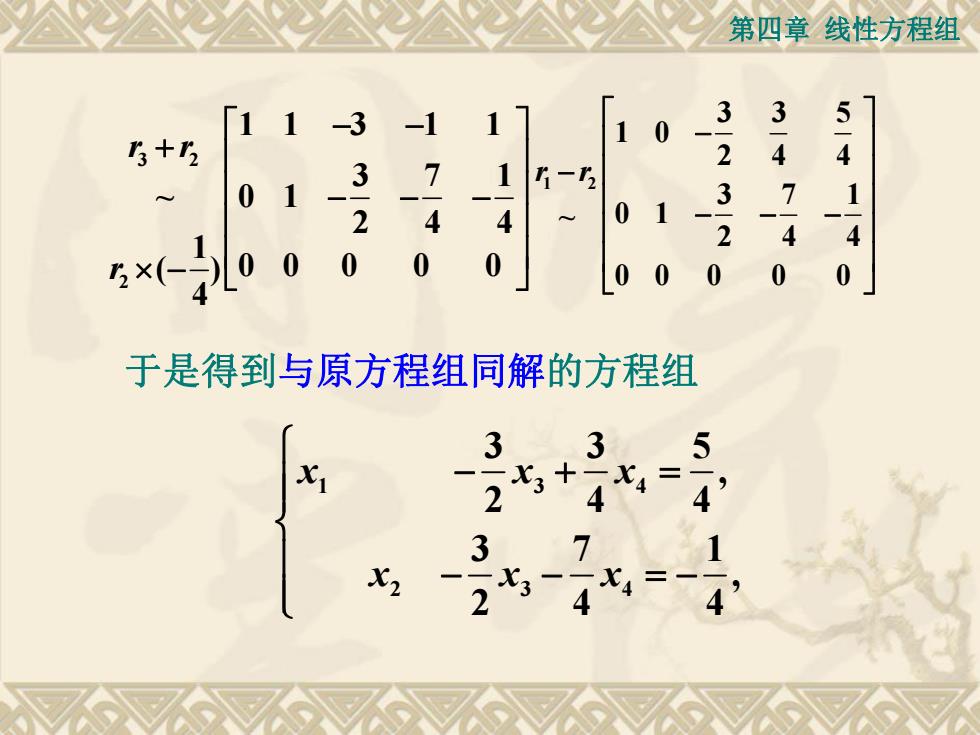
第四章线性方程组 11 -3 -1 3 3+3 2 5-4 3 1 1-3 01 3 7 1 2 4 4 01 2 4 5×(00 0 0 0 0 0 0 0 0 于是得到与原方程组同解的方程组 33 25* 5 4 3 x2 x3-尤4= 4
第四章 线性方程组 3 2 2 1 1 3 1 1 3 7 1 ~ 0 1 2 4 4 1 ( ) 0 0 0 0 0 4 r r r 1 2 3 3 5 1 0 2 4 4 3 7 1 ~ 0 1 2 4 4 0 0 0 0 0 r r 于是得到与原方程组同解的方程组 1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 , 2 4 4 x x x x x x