
I, f(x)dx =-' f(-t)dt =f" f(-t)dt,(1)f(x)为偶函数,则f(-t)= f(t),J" f(x)dx = J~ f(x)dx+ J" f(x)dx=2]" f(x)dx;(2)f(x)为奇函数,则f(-t)=-f(t)I", f(x)dx = J" f(x)dx + f" f(x)dx= 0
− = 0 ( ) a f x dx − − = 0 ( ) a f t dt ( ) , 0 − a f t dt (1) ( ) ( ) ( ), f x f t f t 为偶函数,则 − = 0 0 ( ) ( ) ( ) a a a a f x dx f x dx f x dx − − = + 0 2 ( ) ; a = f x dx (2) ( ) ( ) ( ), f x f t f t 为奇函数,则 − = − − − = + a a a a f x dx f x dx f x dx 0 0 ( ) ( ) ( ) = 0
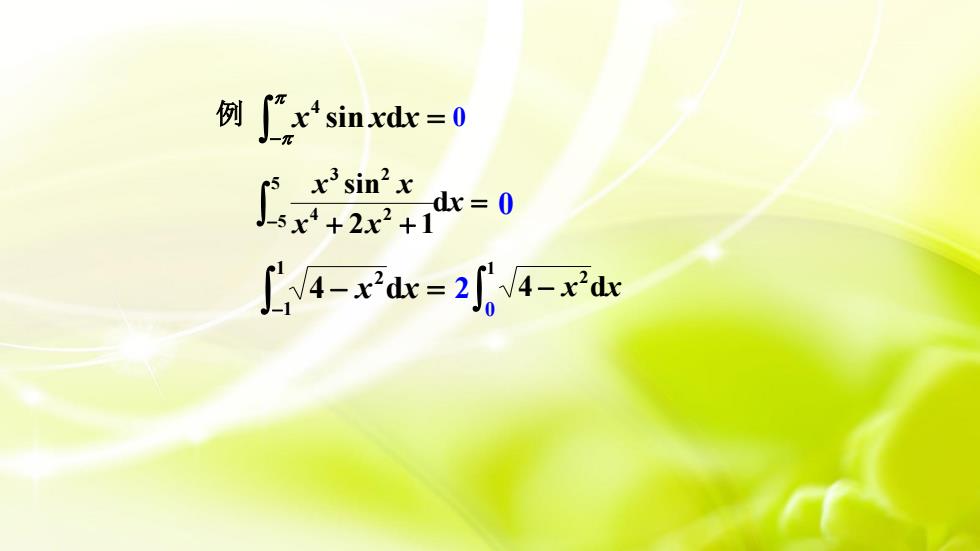
例x sin xdx = 0-元x"sin'xdx = 0-5x4 +2x2 +1IV4-x'dx=2f' 4-x'dx
= − x sin xdx 4 − − = 1 1 2 4 x dx = + + − x x x x x d 2 1 5 sin 5 4 2 3 2 4 x dx 1 2 − 0 0 例 2 0

2x2+xcosx练习 计算[,dx.1+ /1-x22xxcosxde+T解?原式=dx1+/1-x1+V1-x奇函数偶函数tx(1- /1-x2=41+V1-xdx=4f'dx01-(1-x2)=4f(1-/1-x)dx=4+4f" /1-xdx单位圆的面积=4-元
奇函数 练习 计算 解 . 1 1 1 2 cos 1 2 2 − + − dx x x x x 原式 − + − = 1 1 2 2 1 1 2 dx x x − + − + 1 1 2 1 1 cos dx x x x 偶函数 + − = 1 0 2 2 1 1 4 dx x x − − = 1 0 2 2 2 1 (1 ) (1 1 ) 4 dx x x x = − − 1 0 2 4 (1 1 x )dx = − − 1 0 2 4 4 1 x dx = −4 . 单位圆的面积

综日(1) ,x /x/dx奇x//xjdx+(x//x/dx2 dx= =(4/2-1)=0+2A(2) Jdxr1+x?偶奇dxdx+1+x28Y2=0+2dxI1+x?3Jo
= 0 + = + − x | x |dx 1 (4 2 1) 5 2 = − x x x x d 1 2 2 2 5 3 − + − = = 0 + 3 8 = − x | x |dx 2 奇 奇 偶 1 1 x x x x d 1 2 2 2 0 2 4 2 + − − 1 x | x |dx 2 1 ( )− x x x x d 1 2 2 2 2 4 2 − + − − + 2 + 1 2 1 1 x dx x x x x x x d 1 2 (2) 2 2 2 5 4 3 2 − + + − − −

元sinx4dx元一说明:在对称区间上的积分先考虑被积函数的奇偶性,否则做变换x=一会收到很好的效果
说明:在对称区间上的积分先考虑被积函数的奇偶性, 否则做变换x= -t会收到很好的效果. 2 4 4 sin 1 x x dx e − − +