
应用换元公式时应注意:(1)用x=(t)把变量x换成新变量t,积分限也相应的改变,,(换元必换限);(2)求出f[p(t)lp'(t)的一个原函数Φ(t)后,不必像计算不定积分那样把@Φ(t)还原成变量x的函数,而是直接把新变量的上下限分别代入Φ(t)然后相减就行了
应用换元公式时应注意: (1) ( ) 用x t x t = 把变量 换成新变量 ,积分限 也相应的改变,(换元必换限) ; (2) [ ( )] ( ) ( ) ( ) ( ) . f t t t t x t t 求出 的一个原函数 后,不 必像计算不定积分那样把 还原成变量 的 函数,而是直接把新变量 的上下限分别代入 然后相减就行了

计算例1Va?-x'dx解1 令x=asintdx = acostdt元x=0=t=0x=a=t=2Ta’ cos?2 - xdx =tdt0Ta?(1 + cos 2t)dt =2A1
令 2 2 0 a − a x dx 2 2 2 0 cos π = a tdt 2 2 0 (1 cos 2 ) 2 π a = + t dt 2 4 πa = x a t = sin dx a tdt = cos x t = = 0 0 2 π x a t = = 解1 计算 2 2 0 a a x dx − 例 1

0解2由定积分的几何意义[Va?-x"dx0元a?等于圆周的第一象限部分的面积
解2 由定积分的几何意义 2 2 0 a a x dx − 等于圆周的第一象限部分的面积 2 4 πa = a a 2 2 y = a − x x y O
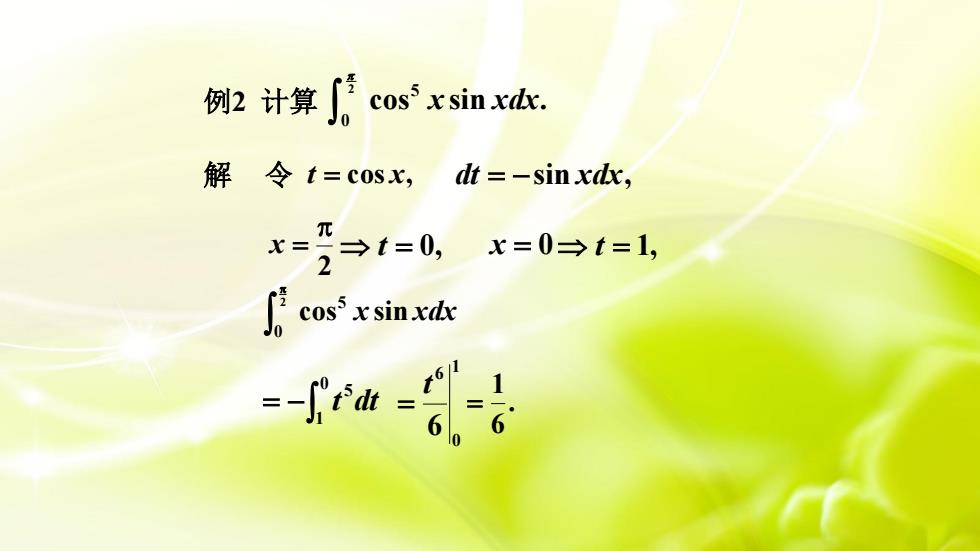
cos' x sin xdx.例2计算0解令dt = -sin xdx,t = cosx,元=→t=0,x=0=t=1,x=122cos' x sin xdxJo
例2 计算 2 5 0 cos sin . x xdx 解 令 t = cos x, 2 x = t = 0, x = 0 t = 1, 2 0 5 cos x sin xdx = − 0 1 5 t dt 1 0 6 6 t = . 6 1 = dt = −sin xdx
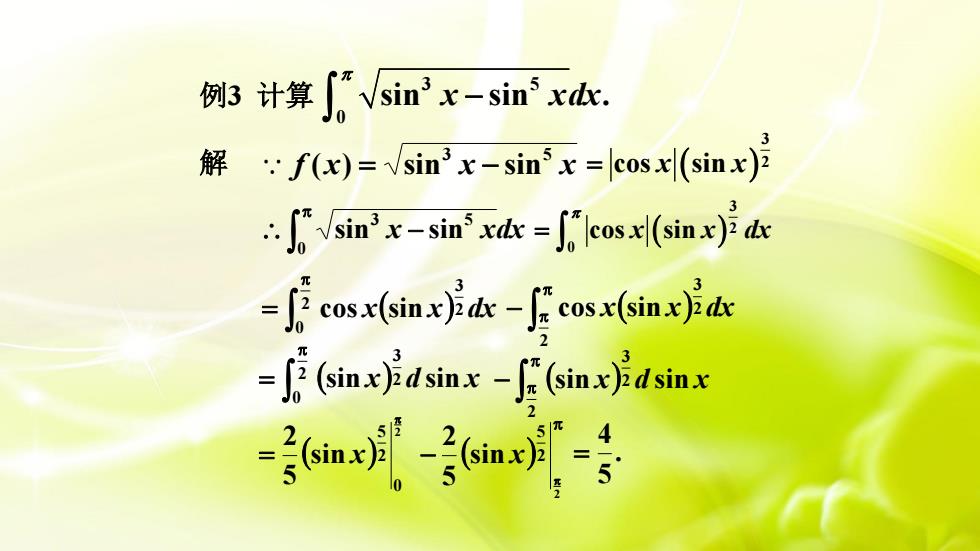
["sin' x - sin' xdx.例3计算解 : f(x)= /sin'x-sin'x =|cosxl(sinx) J"sin'x-sin' xdx=J"cosx(sinx)dxJe cosx(sinx)dx -fu cosx(sinx)idxfe (sinx)d sinx -f" (sinx)id sinx-,(sinx) -号(sinx)=3
例3 计算 解 3 5 0 sin sin . x xdx − f x x x 3 5 ( ) = sin − sin ( ) 3 = cos sin x x 2 − 0 3 5 sin x sin xdx ( ) 3 2 0 cos sin x x dx = ( ) = 2 0 2 3 cos x sin x dx ( ) − 2 2 3 cos x sin x dx ( ) = 2 0 2 3 sin x d sin x ( ) − 2 2 3 sin x d sin x ( ) 2 0 2 5 sin 5 2 = x ( ) − 2 2 5 sin 5 2 x . 5 4 =