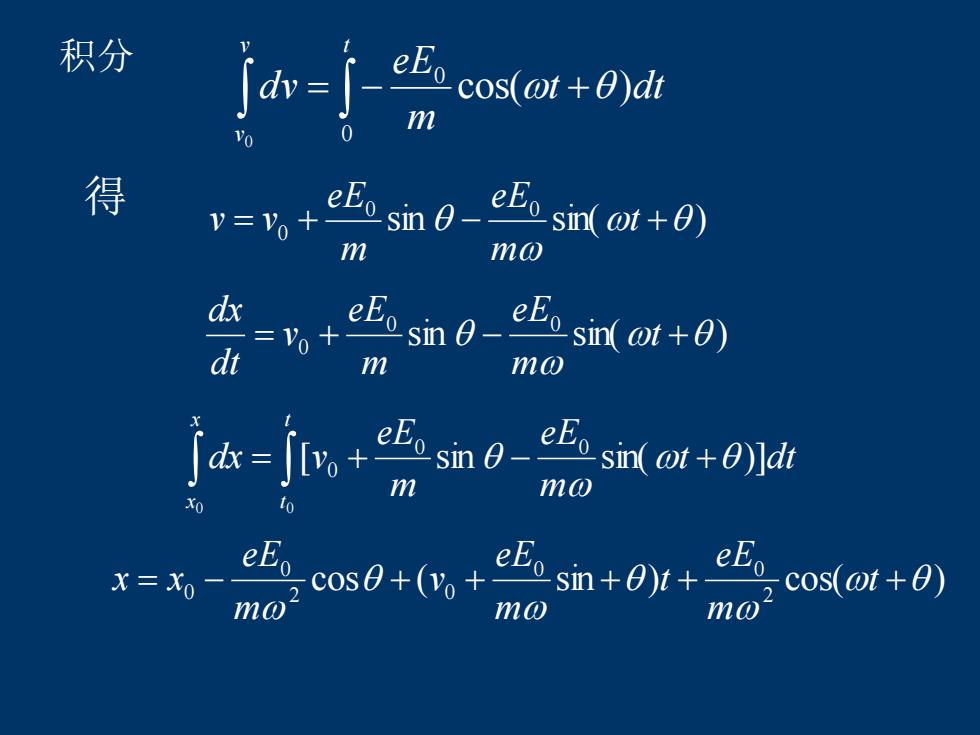
积分 j-ja+0a 得 =+n-c+9) mo =+eEsm0-5smm+9 dx dt m mw 于k=j+a-s+0 m
积分 得 t dt m eE dv v t v cos( ) 0 0 0 = − + sin sin( ) 0 0 0 = + − t + m eE m eE v v sin sin( ) 0 0 0 = + − t + m eE m eE v dt dx t dt m eE m eE dx v t t x x [ sin sin( )] 0 0 0 0 = 0 + − + cos ( sin ) cos( ) 2 0 0 2 0 0 0 = − + + + + t + m eE t m eE v m eE x x

例题2力是速度的函数 在具有阻力的媒质中运动的抛射体 ·分析:受力 mg R ·运动微分方程 mr =mg +R 用自然坐标系分解(运动方向为正) mh=-R-mgsn日 ds dt de m-=mgcose d dv ds dv EV- dt ds dt ds
例题2 力是速度的函数 在具有阻力的媒质中运动的抛射体 • 分析:受力 mg R • 运动微分方程 mr mg R = + = = − − cos ( ) sin 2 mg v m R v mg dt dv m d ds = − ds dv v dt ds ds dv dt dv = = • 用自然坐标系分解(运动方向为正)

dv mv -=-R(v)-mgsin 0 ds v2 112 ds =mgcose do 1 dv R(v)+mgsin 0 两式相比 y do mgcos0 可解出 v=f(0)
= − = − − cos ( ) sin 2 m g d ds v m R v m g ds dv mv 两式相比 可解出 cos 1 ( ) sin mg R v mg d dv v + = v = f ( )

因此: dx dx ds =peos0=-广-Ox=O do ds de 8 8 dydy ds -s-Oy0) do ds do 8 g dt dt ds =-2= vsec0_f(0)sec1=1(0) do ds do 1) g 8 消去参量0 可得运动方程
( ) [ ( )] cos 2 2 x x g f g v d ds ds dx d dx = = − = − = − = ( ) [ ( )] sin 2 2 t g y y g f g v t g d ds ds dy d dy = = − = − = − = ( ) sec ( )sec t t g f g v d v ds ds dt d dt = = − = − = − = 消去参量 可得运动方程 因此:

例题3 力是坐标的函数 原子在晶体点阵中的运动F(x,y,z)=-kx-k,)-kk 运动微分方程: mi=F(x,y,2) mi=-kyx 直角坐标分解: mi=-kyy mi=-k,z 令 初始条件:1=0,x=0,x=A,0 m x=A cos(@t+0) 可解得 y=Acos(0,1+8,) z=A.cos(@.t+0.)
例题3 力是坐标的函数 原子在晶体点阵中的运动 F x y z k xi k yj k zk x y z ( , , ) = − − − mr F(x, y,z) = = − = − = − mz k z my k y mx k x z y x m kx x = 2 Ax x t = 0,x = 0,x = = + = + = + cos( ) cos( ) cos( ) z z z y y y x x x z A t y A t x A t 可解得 令 初始条件: 直角坐标分解: 运动微分方程: