
第3章静定梁和静定平面刚架 3-1一般方法 3-2 多跨静定梁 3-3静定刚架
3-1 一般方法 3-2 多跨静定梁 第3章 静定梁和静定平面刚架 3-3 静定刚架
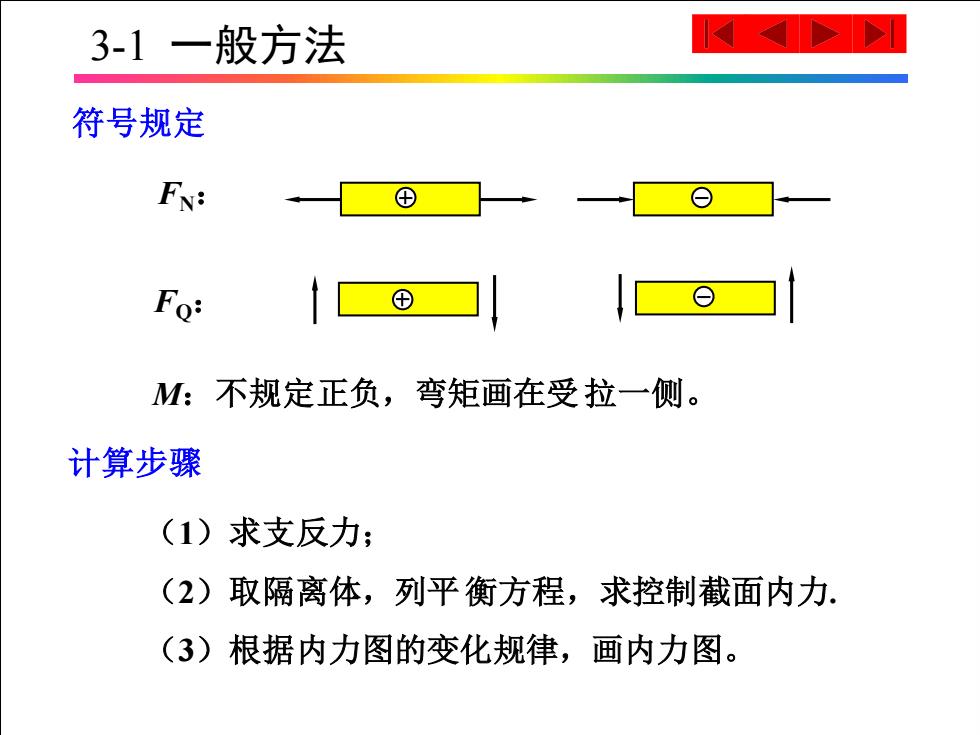
3-1一般方法 IA✉>> 符号规定 FN: ⊕ Fo: ⊕ M:不规定正负,弯矩画在受拉一侧。 计算步骤 (1)求支反力; (2)取隔离体,列平衡方程,求控制截面内力. (3)根据内力图的变化规律,画内力图
3-1 一般方法 符号规定 M:不规定正负,弯矩画在受拉一侧。 FN: FQ: (1)求支反力; (2)取隔离体,列平衡方程,求控制截面内力. (3)根据内力图的变化规律,画内力图。 计算步骤

内力图的变化规律 (a)无均布荷载的区段,Fo图为水平线、M为斜线。 有 -,Fo图为斜直线、M为曲线。 凹向与均布荷载的方向一致。 (b)M图的极值点在Fo=0处或Fo图变号处。 (c)铰出无力偶作用时,M=0; 有- 弯矩等于力偶值。 (d) 集中力作用时,M图是折线;Fo图有突变, 突变值等于作用力。 (ε)集中力偶作用时,M图有突变,突变值等于力偶值
内力图的变化规律 (a)无均布荷载的区段,FQ图为水平线、M为斜线。 有-,FQ图为斜直线、M为曲线。 凹向与均布荷载的方向一致。 (b)M图的极值点在FQ =0处或FQ图变号处。 (c)铰出无力偶作用时,M=0; 有-,弯矩等于力偶值。 (d)集中力作用时,M图是折线; FQ图有突变, 突变值等于作用力。 (e)集中力偶作用时,M图有突变,突变值等于力偶值
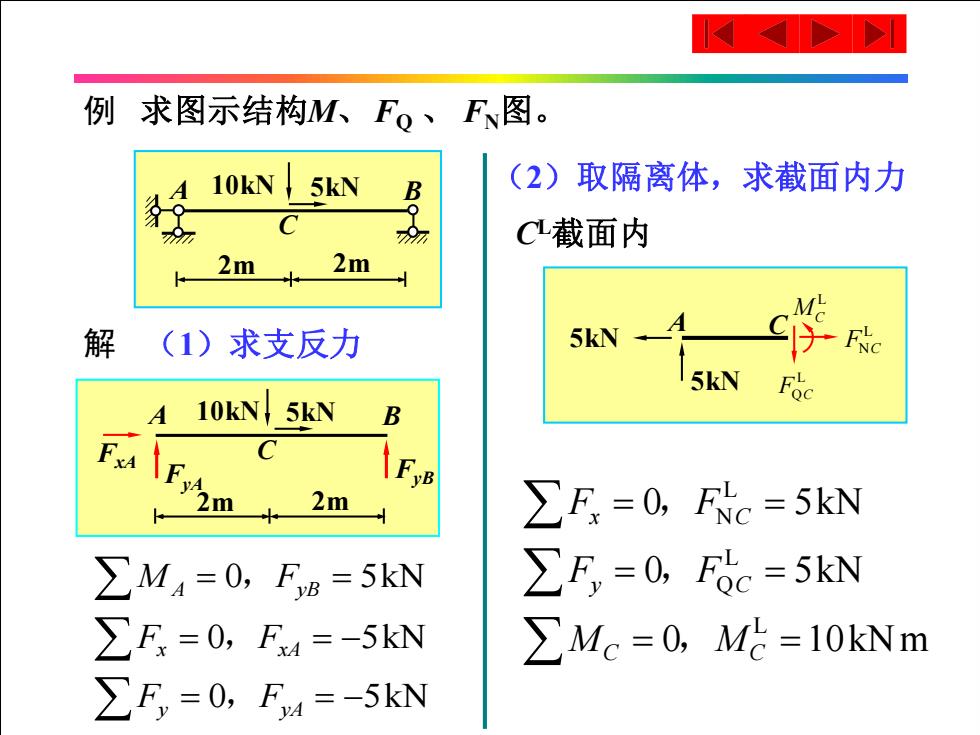
例求图示结构M、Fo、F图。 10kN 5kN B (2)取隔离体,求截面内力 C心截面内 2m 2m M 解 (1)求支反力 5kN C于 5kN Foc 10kN 5kN B C A \FyB 2m 2m ∑F=0,Fkc=5N ∑M4=0,FB=5kN ∑F,=0,Fc=5kN ∑F=0, F=-5kN ∑Mc=0,M=10kNm ∑F,=0, Fy =-5kN
解 例 求图示结构M、FQ 、 FN图。 (1)求支反力 FyB 5kN FyA FxA 2m A 2m 10kN C B (2)取隔离体,求截面内力 CL截面内 5kN 5kN A C L MC L FNC L FQC 0 5kN 0 5kN 0 5kN A yB x xA y yA M F F F F F = = = = − = = − , , , 2m A 2m 10kN 5kN C B L N L Q L 0 5kN 0 5kN 0 10kNm x C y C C C F F F F M M = = = = = = , ,
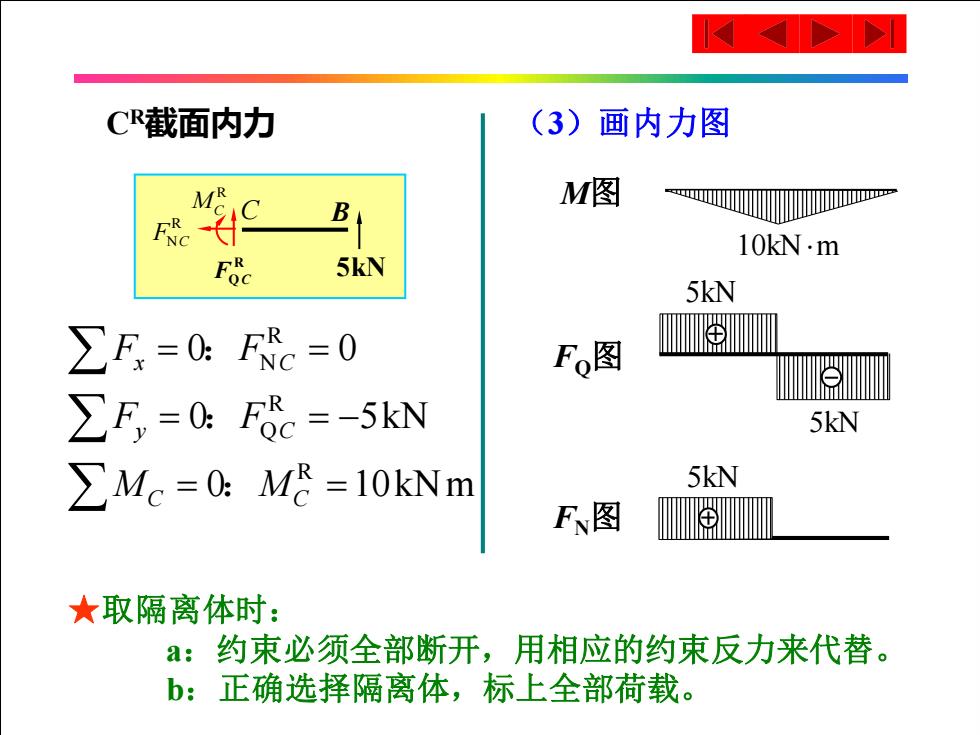
C截面内力 (3)画内力图 9 M图 E 10kN.m Foc 5kN 5kN ∑F=0:Fc=0 Fo图 ∑F=0:F6=-5kN 5kN ∑Mc=0:M&=l0kNm 5kN F图 ★取隔离体时: a:约束必须全部断开,用相应的约束反力来代替。 b:正确选择隔离体,标上全部荷载
CR截面内力 R N R Q R 0 0 0 5kN 0 10kNm x C y C C C F F F F M M = = = = − = = : : : 5kN C B R MC R FNC F C R Q (3)画内力图 M图 10kNm FQ图 FN图 5kN 5kN 5kN ★取隔离体时: a:约束必须全部断开,用相应的约束反力来代替。 b:正确选择隔离体,标上全部荷载