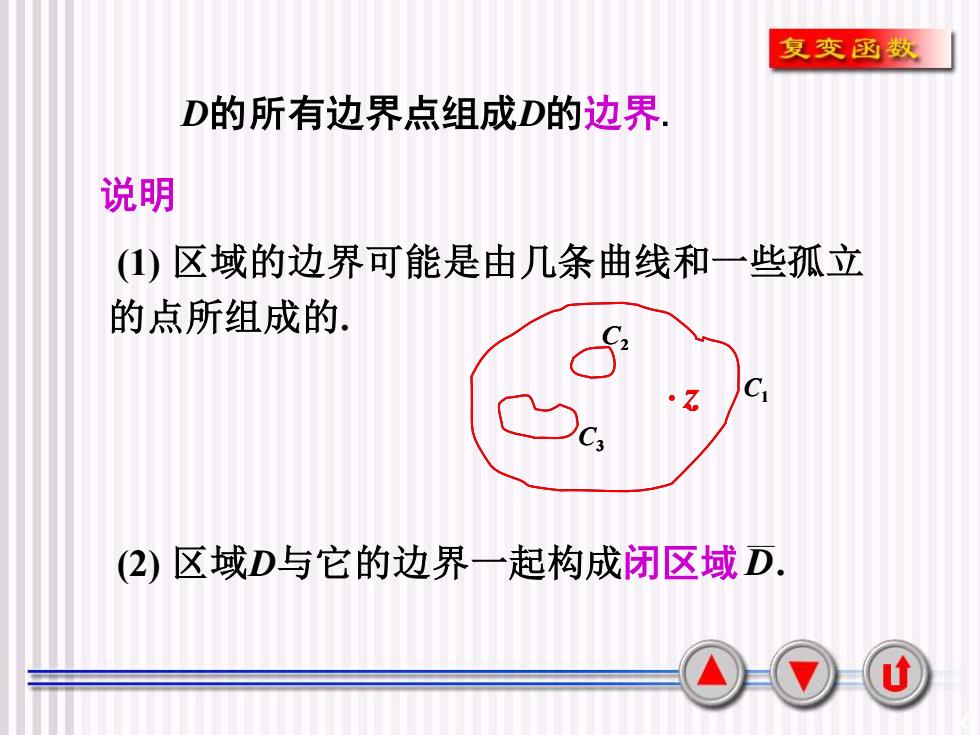
复变函数D的所有边界点组成D的边界说明(1)区域的边界可能是由几条曲线和一些孤立的点所组成的0C:zC(2)区域D与它的边界一起构成闭区域D.u
6 D的所有边界点组成D的边界. 说明 (1) 区域的边界可能是由几条曲线和一些孤立 的点所组成的. (2) 区域D与它的边界一起构成闭区域 D. z C1 C2 C3 z C1 C2 C3
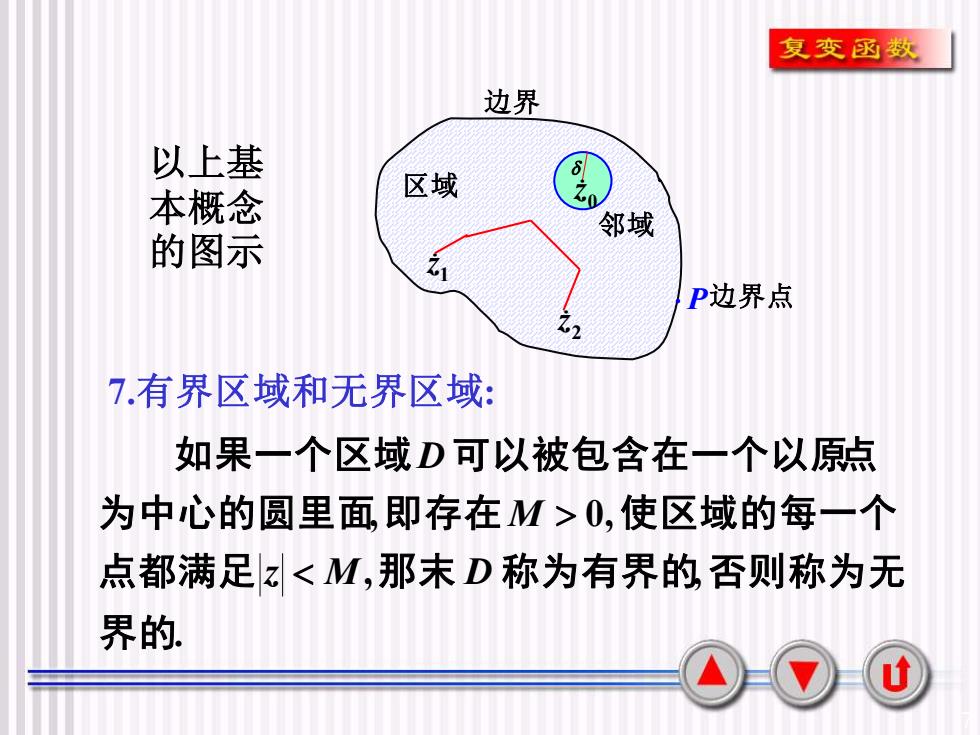
复变函数边界以上基区域本概念邻域的图示4P边界点7.有界区域和无界区域如果一个区域D可以被包含在一个以原点为中心的圆里面,即存在M>0,使区域的每一个点都满足z<M,那末D称为有界的否则称为无界的.u
7 以上基 本概念 的图示 1 z 2 z 区域 0 z 邻域 P 边界点 边界 7.有界区域和无界区域: . , , , 0, 界 的 点都满足 那 末 称为有界的 否则称为无 为中心的圆里面 即存在 使区域的每一个 如果一个区域 可以被包含在一个以原点 z M D M D
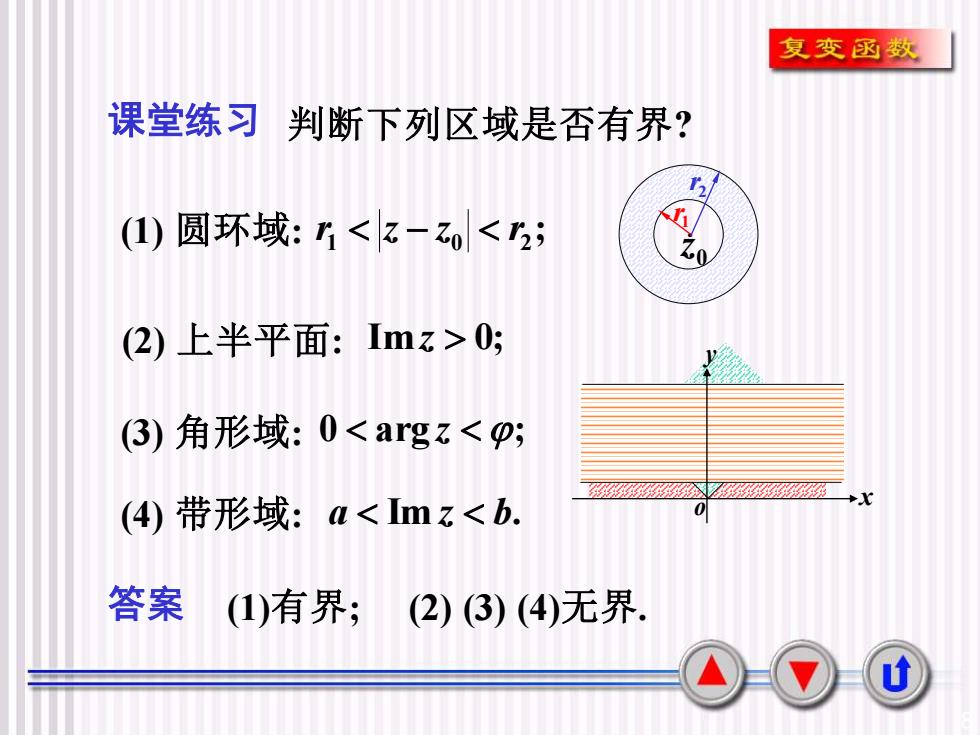
复变函数课堂练习判断下列区域是否有界?1(l)圆环域:r<-zo<r;10(2)上半平面:Imz>0;(3)角形域:0<argz<β;x(4) 带形域: a<Imz<b.答案(1)有界;(2) (3) (4)无界
8 (1) 圆环域: ; 1 0 2 r z − z r 0 z 2r 1r 课堂练习 判断下列区域是否有界? (2) 上半平面: Imz 0; (3) 角形域: 0 arg z ; (4) 带形域: a Im z b. 答案 (1)有界; (2) (3) (4)无界. x y o