
主进 方本 第二节 数列的极限 一 数列极限的定义 二、 收敛数列的性质
山东农业大学 高等数学 主讲人:苏本堂 第二节 数列的极限 一、 数列极限的定义 二、 收敛数列的性质
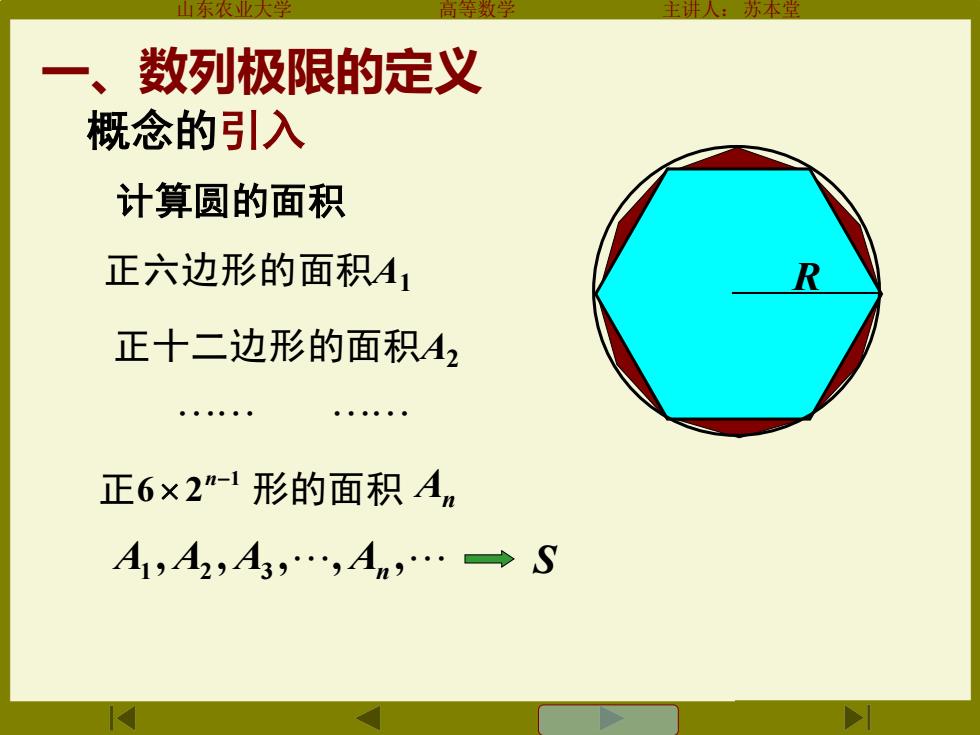
东 一、数列极限的定义 概念的引入 计算圆的面积 正六边形的面积A 正十二边形的面积A2 。 。● 正6×2”-1形的面积Am A1,A2,A3,.,A,.→S
山东农业大学 高等数学 主讲人:苏本堂 一、数列极限的定义 概念的引入 正六边形的面积A1 R 正 6 2 n−1 形的面积 An A1 , A2 , A3 , , An , S 正十二边形的面积A2 计算圆的面积

1.数列的概念 按照某一法则,对每一neN+,对应着一个确定的实数 x,则得到一个序列 X13X22X3)···,Xn3· 这一序列叫做数列,记为{x},第n项xn叫做数列的一般项 2,4,8,.,2,.;1,-1,1,.,(-1)+1,. 1111 2'4'82n. 2,14.n+(-1)-1 22’3 注意:(1)数列对应着数轴上一个点列可看作一动 点在数轴上依次取X1,X2,.,Xn,. X3 X1 x2 X4 n (2).数列是整标函数xn=f(n),n∈N+
山东农业大学 高等数学 主讲人:苏本堂 1. 数列的概念 按照某一法则, 对每一nN+ , 对应着一个确定的实数 xn , 则得到一个序列 x1 , x2 , x3 , , xn , , 这一序列叫做数列,记为{xn }, 第n项xn叫做数列的一般项. 2, 4, 8, , 2 n , ; 1, −1, 1, , (−1) n+1 , . , ; 2 1 , , 8 1 , 4 1 , 2 1 n , ; ( 1) , , 3 4 , 2 1 2, 1 n n n− + − 注意: (1).数列对应着数轴上一个点列.可看作一动 点在数轴上依次取 , , , , . x1 x2 xn 1 x3 x x2 4 x n x (2).数列是整标函数 x f (n), n = . + n N

引 观察数列1+-}当n→∞ 时的变化趋势 通过观察:当m无限增大时,x,=1+) 无限接近于1. 问题:“无限接近”意味着什么?如何用数学语言刻划它 x-1=(-1)-=1 nn 给定 由1<1 100,只要n>100时,有x,-1< 00 给定 1 10000'只要n>10000时,有x,-1<, 10000 给定>0,只要n>N(=日时,有x-1<e成立
山东农业大学 高等数学 主讲人:苏本堂 问题:“无限接近”意味着什么?如何用数学语言刻划它. 通过观察:当n无限增大时, n x n n 1 ( 1) 1 − − = + 无限接近于1. 引例 观察数列 } ( 1) {1 1 n n− − + 当n → 时的变化趋势. , 100 1 给定 , 100 1 1 n 由 只要 n 100时, , 100 1 有 xn − 1 , 10000 1 , 有 xn − 1 10000 1 给定 只要 n 10000时, 给定 0, ]) , 1 只要 ( [ 时 n N = 有 − 1 成立. xn xn − 1 = n n n 1 1 ( 1) 1 − = −

2.数列极限的通俗定义 当n无限增大时,如果数列{xm}的一般项xn无限接近 于常数a,则常数a称为数列{xn}的极限,或称数列{xn}收 敛a,记为 lim xn=a 当n无限增大时,xn无限接近于a. 一当n无限增大时,xm-a无限接近于0 →当n无限增大时,xna可以任意小,要多小就能有多小. 一当n增大到一定程度以后,x,-d能小于事先给定的任意 小的正数, 因此,若n增大到一定程度以后,xna能小于事先给 定的任意小的正数,则当n无限增大时,x,n无限接近常数a
山东农业大学 高等数学 主讲人:苏本堂 2. 数列极限的通俗定义 当n无限增大时, 如果数列{xn }的一般项xn无限接近 于常数a, 则常数a称为数列{xn }的极限, 或称数列{xn }收 敛a, 记为 xn a n = → lim . 当n无限增大时, xn无限接近于a . 当n无限增大时, |xn -a|无限接近于0 . 当n无限增大时, |xn -a|可以任意小, 要多小就能有多小. 当n增大到一定程度以后, |xn -a|能小于事先给定的任意 小的正数. 因此, 若 n 增大到一定程度以后, |xn -a|能小于事先给 定的任意小的正数, 则当n无限增大时, xn无限接近常数a