
20、《高等数学》(第七版)上册习题全解取X=maxX,X,则当lx>X即x>X或x<-X时,就有f(x)=A<e即limf(x)=A.11.根据函数极限的定义证明:函数f(x)当x一→xo时极限存在的充分必要条件是左极限、右极限各自存在并且相等证必要性若limf()=A,则V>0,38>0,当0<1x-x1<时,就有If(x)-AI<8.特别,当0<x-xo<时,有1f(x)-A1<,即limf(x)=A;当0<x-x<时,有If(x)-AI<,即limf(x)=A充分性若lim(x)=A=limf(x)则V>0,日8>0当0<x-x<8时,就有f)<又8>0,当0-x,时就有F()-AI<.取=min(8,02/则当0<1x-x<8时,就有1f(x)-Al<即limf(x)=A*12.试给出x一时函数极限的局部有界性的定理,并加以证明,解局部有界性定理如果limf(x)=A,那么存在常数M>0和X>0,使得当Ix|>X时,有If(x)|≤M.证明如下:因为limfx)=A,所以对=1>0,3X>0,当1x1>X时,就有I(α)-AI<1,从而IF(x)I≤U(x)-AI+IAI<I+IAI,取M=1AI+1,即有当1xl>X时,I(x)/≤M习题1-4无穷小与无穷大F1.两个无穷小的商是否一定是无穷小?举例说明之解不一定.例如,α()=2×与β(*)=3x都是当0时的无穷小,但()β(x)2却不是当x一0时的无穷小32.根据定义证明:x2-9为当x-3时的无穷小;(1)yx+31(2)y=xsin为当x-0时的无穷小-x2-9证(1)因为=1x-31,所以Vg>0,取8=e,则当0<1x-31<8时,x+3就有

21第一章函数与极限98机为当x-3时的无穷小x+3(2)因为xsin≤1xl所以V>0取=,则当0<1l<8时,就有1xsinEY即xsin为当x-→0时的无穷小,1"3.根据定义证明:函数=+2*为当x=0时的无穷大.问应满足什么条件,能使xyl >104?1+2元1+2证因为>M,只要要使2 >M,xx111+2x>M即|x|<所以VM>0取8=,则当0<1x-01<8时,就有M+2M+2x即+2*为当x→0时的无穷大。x11+2>104令M=104取8=时,就能使当0<1x-01104+2'10*+2x1+2x注在本题的证明中,采取先将If(x)1等价变形,然后适当缩小,使x缩小后的量大于M,从而求出6.这种方法在按定义证明函数在某个变化过程中为无穷大时,也是经常采用的4.求下列极限并说明理由:2x+11-x2(1) lim(2) limx(1) lim2x +1_1解x为当×-→时的无穷小;再由定理1,lim理由:由定理2,1 -x2= lim(1 +x) =1.(2)lim-01-x理由:由定理1,lim(1+x)=1.5.根据函数极限或无穷大定义,填写下表:
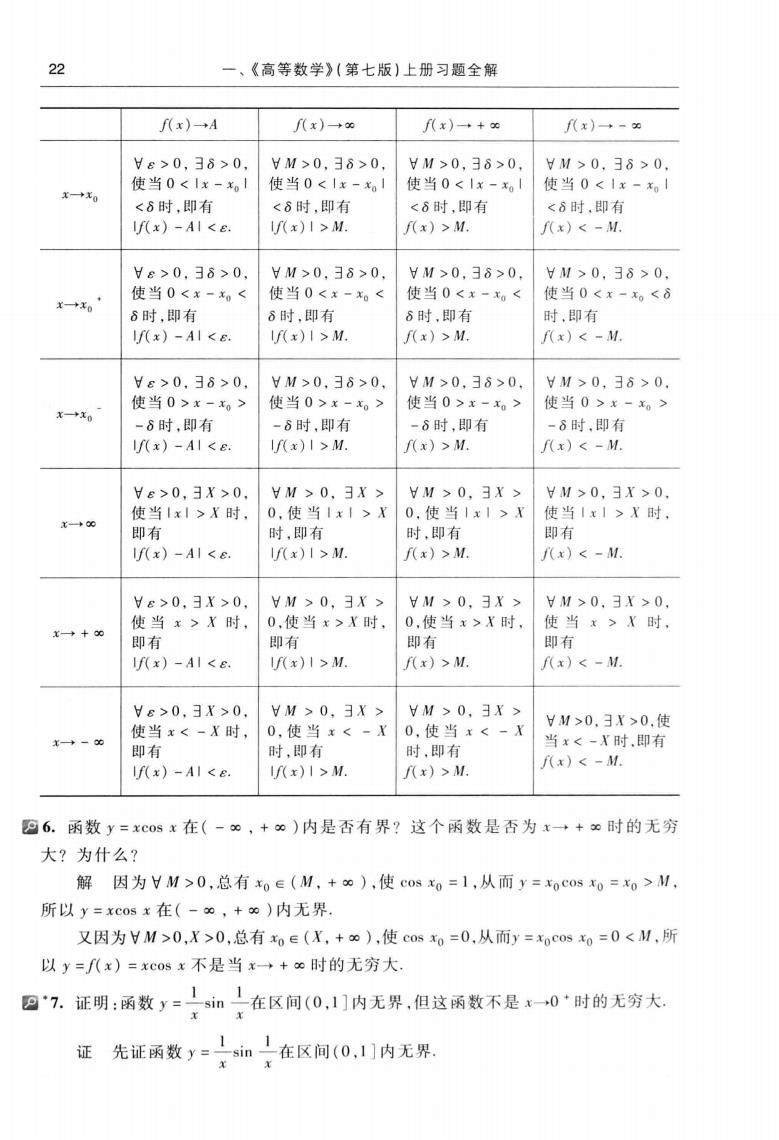
22《高等数学》(第七版)上册习题全解f(x)-→A(x)+00f(x)→+(x)-αVe>0,38>0,VM>0,38>0.M>0,30>0,0.30使当0<1x-x1使当0<1x-x1使当01x-使当0<1x-1X+30<8时,即有<8时,即有<6时,即有<8时,即有I(x) 1 >M.f(x) >M.F(x) <-M.If(x)-AI<E.V8>0.8>0,VM>0.38>0.VM>0,38>0.VM>0.38>0.使当0x-使当0<使当0x-x<使当0<x-x。<ox-→+xo8时,即有时,即有6时,即有时,即有I(x)1 >M.F(x)>M.J(x)<-M.IF(x)-AI<Ee>08>0.VM>0.38>0.VM>0,38>0.VM>0.8>0.使当0>>使当0>->使当0>>使当0>x-x。+x0-8时,即有-8时,即有-8时,即有-8时,即有I(x) I >M.J(x)>M.J(x)<-M.I(x) -AI<8.Ve>0,3X>0.VM>O.EX>>OE>VM>0,EX>0.使当1xl>X时,0.使当1x1>X0.使当1x1>X使当Ix>X时,→00即有即有时,即有时,即有(x)<-M.(x)1>M.f(x) >M.If(x)-Al<eVE>0,3X>0.VM>O,3X>M>E>VM>0,3X>0.使当x>X时,0.使当x>X时,0.使当x>X时,使当x>X时,+0即有即有即有即有(x)>M.f(x)<-M.U(x)1 >M.If(x) -Al <e.Vg>0.3X>0.VM>O.3X>VM>O.EX>VM>0.3X>0.使使当x<-x时,0.使当x<-X0.使当x<-x当-X时,即有OC即有时,即有时,即有(x)<-M.1(x)1 >M.J(x)>M.If(x)-AI <86.函数y=xcosx在(-80,+)内是否有界?这个函数是否为x-→+8时的无穷大?为什么?解因为VM>0,总有xoe(M,+),使cosx=1,从而y=xocosxo=xo>M,所以y=xcosx在(-,+)内无界又因为VM>0,X>0,总有xoe(X,+),使cosxo=0从而y=xocosxo=0<M,所以y=f(x)=xcosx不是当x-→+时的无穷大,11在区间(0,11内无界,但这函数不是x一0时的无穷大*7.证明:函数y=sinxX11一在区间(0,11内无界)证先证函数Yxx

23第一章函数与极限-因为VM>0.在(0.1]中总可找到点xo,使f()>M.例如,可取xoke2k元+号211N),则(xo)=2k+号,当充分大时,可使(xo)>M.所以y=在(0,11内无界)sin再证函数y=(x)=sin一不是x→0*时的无穷大。xX因为M>0,8>0,总可找到点x0,使0<x<8,但f)<M.例如,可取x=L(kEN+),当k充分大时,0<x<8.但f(x)=2kmsin2k㎡=0<M.所以2km1一不是×→0+时的无穷大,sinxx48.求函数f(x)的图形的渐近线,2-解因为limf(x)=0,所以y=0是函数图形的水平渐近线因为limf(x)=,limf(x)=α,所以x=-/2及x=/2都是函数图形的铅直渐近线,习题1-5极限运算法则1.计算下列极限:x2+5x2-3(2) lim(1)limx-3-斤2+1x2-2x+14x3-2x2+x(4) lim(3)limx2-13x2+2x(x+h)2-x2(6) lim(2 --(5)lim-+);福-h2_1x2+x(7)lim(8)lim*2x2-x-*x4-3±2+1x2-6x+8(10) lm(1+)(2-);(9)lim4x2-5x+4(12) imI+2 +3 +.+(n -1),(11) lim(1 +24n2(n+1)(n+2)(n+3)3(13)lim(14) lim1-x1-x35n3lim(x2 +5)x2+59解(1)lim-9.-1x-3lim(x-3)

24、《高等数学》(第七版)上册习题全解lim(x2-3)x2-30E(2)lim=045x2+1lim(x?+1)5lim(x-1)x2-2x+1(x-1)20=limz-1=lim(3)lim=02x?-1-(x-1)(x+1)-1x+1lim(x+1)Elim(4x2-2x+1)4x3-2x2+x4x2-2x+11=lim(4) lim23x2+2x3x+2lim(3x+2)a3+0(5) lim(x + h)-12h(2x+h)lim=lim(2x+h)=2xhh4-0A--06-01111(6)lim=lim2lim+ lim=2-0+0=2*+2xrx1I1 limt2Xx2 -11=lim(7)lim1+~*2元21/x-1122lim(x2tx+1111lim++2x3x2 +x0=lim=0(8)lim3131x4-3x2+111lim(1+X242+mlim(x-2)x2-6x+8x-22(x-4)(x-2)=lim=lim(9)lim3lim(x-1)1-4(x-4)(x-1)1-4x-1*x2-5x+4(10) m(1+)(2-)=lm(1+)· Im(2-)=1 ·2=2.1124+11(1) (+++++=limlim2三1242n+n321 lm2)=22m(1)1+2+3+**+(n-1)(12)limn?2n2anm(+1)(2)(n+3)=m(1+)(1+)(1+)(13)lim5n35+0(+)(++)(1+业)151+*+**-3-lim-(x-1)(x+2)(14) limlim1-x3-(1-x)(1 +x+x2)-x1-