
第一章15函数与极限laln2+a所以V>0不妨设要使取&.即n412n28/n2+a2n2+a2则当n>N时,就有Ke即lim1nn(4)因为[0.9999-1|=,要使10.99-118,只要一<e.即10″10″1,所以V>0(不妨设e<1),取N=[1g]则当n>N时,就有10.9999-11<n>lg8.即lim0.999...9=1.6.若limu,=a,证明limlu,1=lal.并举例说明:如果数列1x,!1有极限,但数列x,未必有极限证因为limu,=a,所以Vg>0,日N,当n>N时,有lun-al<e,从而有llu,l-lall≤lu,-al<e,故lim|u,1=lal.但由limlu,1=lal并不能推得limu。=a.例如,考虑数列1(-1)",虽然liml(-1)"|=1,但1(-1)"没有极限,7.设数列1x,1有界,又limy=0,证明:limxnyn=0.证因数列1x有界,故日M>0,使得对一切n有1xl≤M.Ve>0,由于limy>0.3N,当n>N时,就有Iy,I<e1三从而有0.故对81VMIxya-01=lx,1-ly,l<M.=8M所以lim x,yn =0.8.对于数列/x。/,若x2-1→a(k→),x2ka(k-),证明:x-a(n00)证因为x2k-1a(→),所以Vg>0,日,当>,时,有1x2k--al<e;又因为x2h-a(→),所以对上述>0日2,当>kz时,有lx2=al<记K=maxikl,kzl,取N=2K,则当n>N时,若n=2k-1,则k>K+>k,=lx,-al=1x2k-1-al<e,若n=2k.则k>K≥k2=1xn-al=lx2h-al<e.从而只要n>N,就有lxn-al<e,即limx=a
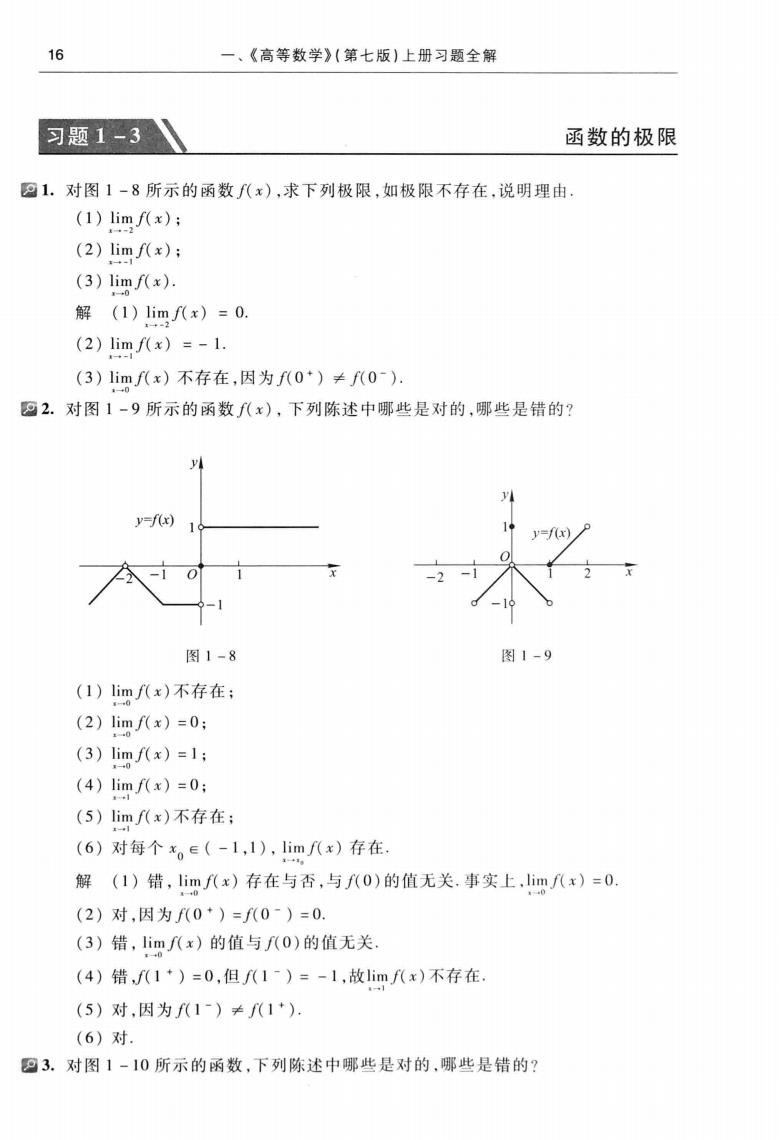
16、《高等数学》(第七版)上册习题全解习题1-3函数的极限1.对图1-8所示的函数(x),求下列极限,如极限不存在,说明理由,(1) limf(x);(2) limf(x);(3) limf(x).解(1)limf(x)=0.(2) limf(x) = - 1.(3)limf(x)不存在,因为f(0+)≠f(0-)2.对图1-9所示的函数f(x),下列陈述中哪些是对的,哪些是错的?川y=f(x)=f(x)x图1-8图1-9(1)limf(x)不存在;(2)limf(x)=0;(3) limf(x) =l;(4)limf(x)=0;(5)limf(x)不存在;(6)对每个x。E(-11),lim/(x)存在解(1)错,limf(x)存在与否,与f(0)的值无关事实上,limf(x)=0(2)对,因为F(0+)=f(0-)=0(3)错,lim(x)的值与(0)的值无关(4)错,f(1+)=0,但f(1=)=-1,故limf(x)不存在,(5)对,因为f(1=)≠(1+)(6)对.3对图1-10所示的函数,下列陈述中哪些是对的,哪些是错的?

17第一章函数与极限=(x)2x01图1-10(1)limf(x)=1;(2)limf(x)不存在;(3)lim(x)=0;(4)limf(x)=l;(5) limf(x)=1;(6)limf(x)=0;(7)limf(x)=0;(8)limf(x)=0.解(1)对.(2)对,因为当x<-1时f(x)无定义(3)对,因为f(0+)=f(0-)=0.(4)错,limf(x)的值与/(0)的值无关(5)对(6)对.(7)对.(8)错,因为当×>2时,(×)无定义,(2+)不存在1xX当x—→0时的左、右极限,并说明它们在×-→0时的极限是,9(x)=4.求f(x)=Y4否存在limJ(x)=lim==lim1=1,lim(x)=lim==lim1=1.解XX+因为limf(x)=1=lim(x),所以limf(x)=1IxlIxl-x=lim-lim(x)=lim=1,limp(x)=lim=lim-140xx1--0因为lim(x)±limp(x),所以lim(x)不存在,5.根据函数极限的定义证明:(1)lim(3x-1)=8;(2)lim(5x+2)=12;

18、《高等数学》(第七版)上册习题全解1 -4x2x2 4(3) lim(4)lim4;22x+12x+2-解(1)因为1(3x-1)-81=13x-91=31x-31要使1(3x-1)-81<8,只要1x-3<号,所以Ve>0,取8=号=,则当0<1x-31<83时,就有1(3x-1)-81<,即lim(3x-1)=8(2)因为1(5x+2)-121=|5x-101=5/x-2要使|(5x+2)-121<e,只要1×-21<E,所以V8>0.取8=-则当01x-2/<8时,就有1(5x+2)-121<8,即lim(5x+2)=12.(3)因为x-→-2,x丰-2,*2-4-(-4)=1x-2-(-4)1=|x+2I=1x-(-2)1x+2要使2-4-(-4)<E+2只要x-(-2)1<e.所以Ve>0,取8=,则当01x-(-2)1<8时.就有12-44- (-4)<EX+2x2-4即lim4x+21(4)因为x2214x2-22= [1 -2x -2|= 2 -(-)2x+1要使1-4x2<e2x+1号,所以Ve>0,取8=号则当0-(-)<8时,就有只要×-(-号)[1 4x22x+11 4x2即lim=22x+1*6.根据函数极限的定义证明:

19第一章函数与极限1 + x31sin x=0(1)lim(2)lim2x3/x11+x31+x31证(1)因为要使E,只要142/x/3)222x32x3111即|x1所以>0,取X,则当1xl>X时,就有<.2/x/3V2V2e1 + *31 +x311即lim622x322x3sin xsinx<6,只要!110,要使1(2)因为<e,即x>,所以VxVxJxx8sinxsin ×=0.Ve>0.取X=,则当x>X时,就有<e.即limVxex*7.当x-→2时,=×24.问8等于多少,使当1x-21<8时,1y-4l<0.001?解由于x-2,1x-21-0,不妨设lx-21<1即1<x<3要使1x2-41=1x+211x-21<51x-21<0.001,只要1 x - 2 / <0. 001=0.0002,5取6=0.0002,则当0<1x-21<8时,就有1x-41<0.001注本题证明中,先限定1x-21<1,其目的是在1x2-41=|x+21×-21中,将1x+21放大为5.从而去掉因子1x+21,再令51x-2<8,由此可以求出1x-21<号,从而找到8.这在按定义证明极限时,也是经常采用的一种方法,5x2 -1*8.当x-时y+1.问X等于多少,使当lxl>X时,1y-11<0.01?x2+3x2-144x2-1<0.01,只要4解因为要使42,x2+332+3+3x20.01,即|xl>20,取X=20,则当1xl>X时,就有1y-11<0.01*9.证明函数(x)=1×1当×-→0时极限为零证因为11x1-01=x1=1x-01所以V>0,取8=6,则当0<[x-018时,就有1|x/-01<e,即limlx|=010.证明:若%-+80及x→-α8时,函数(x)的极限都存在且都等于A,则lim/(x)=A.证因为limx)=A,所以Ve>0,3X,>0,当x>X,时,就有I(x)-AI<E.又因为lim(x)=A,所以对上面的e>0,日X,>0,当x<-X,时,就有If(x)-AI<E