
10一、《高等数学》(第七版)上册习题全解解当0≤t≤1时,S(t)=(2 -0)2= -号 +21 -1,当1<1≤2时,S()=1-22当t>2时,S(t)=1故10瓜I瓜一,2S(t) =12+21-1, 1<1≤2,(1,t>2.16.求联系华氏温度(用F表示)和摄氏温度(用C表示)的转换公式,并求(1)90°F的等价摄氏温度和-5°C的等价华氏温度:(2)是否存在一个温度值,使华氏温度计和摄氏温度计的读数是一样的?如果存在,那么该温度值是多少?解设F=mC+b,其中m,b均为常数因为F=32°相当于C=0°F=212°相当于C=100°所以212-32=1.8b=32.m=100J故F=1.8C+32或C=(F-32).95(1)F=90°,C=(90-32)~32.2°9C=-5°,F=1.8×(-5)+32=23°(2)设温度值符合题意,则有1=1.8t+32,t=-40即华氏-40°恰好也是摄氏-40°17.已知Rt△ABC中,直角边AC、BC的长度分别为20、15,动点P从C出发,沿三角形边界按C→B-A方向移动:动点Q从C出发,沿三角形边界按C-→AB方向移动,移动到两动点相遇时为止,且点Q移动的速度是点P移动的速度的2倍.设动点P移动的距离为x,△CPQ的面积为y,试求y与x之间的函数关系解因为AC=20,BC=15,所以,AB=202+152=25由20<2·15<20+25可知,点P、Q在斜边AB上相遇令x+2x=15+20+25,得x=20.即当x=20时,点P、Q相遇.因此,所求函数的定义域为(0,20).(1)当0<x<10时,点P在CB上,点Q在CA上(图1-5)
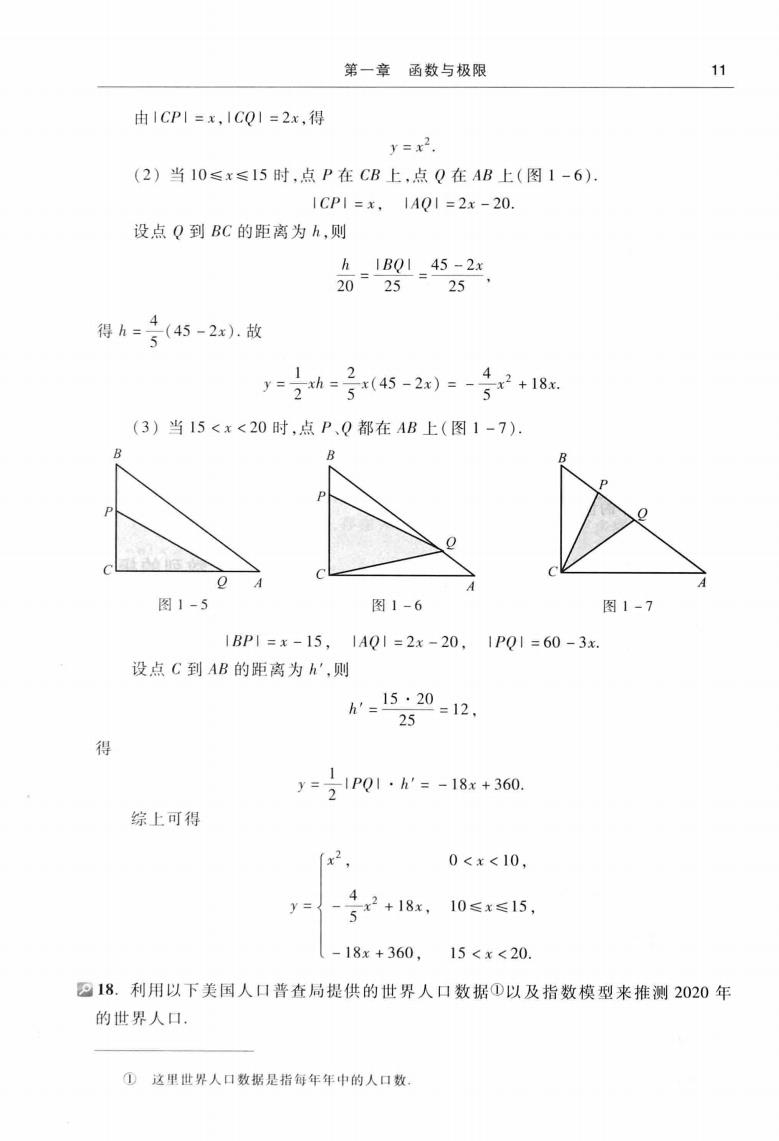
第一章函数与极限11由IcPI=x,ICOI=2x,得y=x2.(2)当10≤x≤15时,点P在CB上,点Q在AB上(图1-6)ICPI=x,1A0I=2x-20设点O到BC的距离为h,则hIBQI452x2025254(45-2x).故得h52142+18x.x(45-2x):-xh =y255(3)当15<x<20时,点P0都在AB上(图1-7).BBA图1-5图1-6图1-7IBPI=x-15,1AQ1=2x-20,1PQ=60-3x设点C到AB的距离为h,则15·20h'==12,25得-IPQ1-h=-18x+360.2综上可得x20<x<10,4元2+18x,10≤x≤15,y=5-18x+360,15<x<2018.利用以下美国人口普查局提供的世界人口数据①以及指数模型来推测2020年的世界人口,①这里世界人口数据是指每年年中的人口数

12一、《高等数学》(第七版)上册习题全解年份人口数(百万)年增长率(%)20086708.21.16620091.1406786.420106863.81.12120116.940.71.10720127017.51.10720137095.2解由表中第3列,猜想2008年后世界人口的年增长率是1.1%,于是,在2008年后的第t年,世界人口将是p(t)=6708.2×(1.011)(百万)2020年对应t=12,于是p(12)=6708.2×(1.011)12~7649.3(百万)76(亿)即推测2020年的世界人口约为76亿习题1-2数列的极限1,下列各题中,哪些数列收敛,哪些数列发散?对收敛数列,通过观察x,的变化趋势,写出它们的极限:(1) ()(2) [(-1)"];(3) [2+);(4)[);[2"-16)(5) (n(-1)"};3#(8)[[(-1)"+1]"+1(7) [n--(1)收敛,liml解=0.-2n(2)收敛,lim(-1)"二=0.(3)收敛,lim(2+=2n-l(4)收敛,lim=1an+l(5)1n(-1)"发散

13第一章函数与极限(6)收敛,lim2"—=0.3″7)发散-1)"+1n+1发散(8)2.(1)数列的有界性是数列收敛的什么条件?(2)无界数列是否一定发散?(3)有界数列是否一定收敛?解(1)必要条件(2)一定发散(3)未必一定收敛,如数列(-1)"1有界,但它是发散的3,下列关于数列x,的极限是a的定义,哪些是对的,哪些是错的?如果是对的,试说明理由:如果是错的,试给出一个反例(1)对于任意给定的e>0,存在NeN.,当n>N时,不等式x,-a<e成立;(2)对于任意给定的ε>0.存在NN.,当n>N时,有无穷多项x,,使不等式Ix,-al<e成立:(3)对于任意给定的e>0,存在NeN+,当n>N时,不等式Ix,-al<ce成立,其中c为某个正常数:(4)对于任意给定的meN,存在NeN,当n>N时,不等式Ix-al<一成立,解(1)错误.如对数列(-1)"+,a=1.对任给的e>0(设e<1),存在N=当n>N时,(-1)"+-1≤<6,但[(-1)”+)的极限不存在nn(2)错误.如对数列n=2k-1,NkeN+,a=l.:n=2k,对任给的e>0(设e<1),存在N=,当n>N且n为偶数时,lx,-al=成立,但,的极限不存在(3)正确.对任给的e>0,取一e>O按假设,存在NEN+,当n>N时,不1等式lx.-al<c.=e成立

14、《高等数学》(第七版)上册习题全解(4)正确.对任给的ε>0.取mEN使<&.按假设,存在NeN.当n>N时,不等式1x-al<<8成立m1os.问limx=?求出N,使当n>N时,,与其4.设数列1x的一般项x,=co21极限之差的绝对值小于正数e.当&=0.001时,求出数N.解limx,=0.证明如下:因为1nT1Ix.-01cos2nn/要使1x,-01<8,只要一所以V>0(不妨设<1),取N=<E.即n>2当n>N时,就有lx-0l<g当e=0.001时,取N==1000.即若=0.001,只要n>1000,就有1x,-01<0.001*5.根据数列极限的定义证明:3n+1.31(1) lim-=0;(2)lim*2n+1"2;*"n2n?+a?(3)lim(4)limo.999...9=1.=1;n0t111-0证(1)因为要使<e只要n>所以Ve0(不妨设e<1)42n2Ve110取N则当n>N时,就有<e.即lim=022313n+13/13n+1,要使<e只要<e.即(2)因为2n+124n2n+1222n+1)4n1(不妨设一.取N=,则当n>时,就有所以>0n>4g3n+133n+13<e,即lim*2n+1=22n+12注本题中所采用的证明方法是:先将1x,-α1等价变形.然后适当放大,使N容易由放大后的量小于ε的不等式中求出.这在按定义证明极限的问题中是经常采用的(3)当a=0时,所给数列为常数列,显然有此结论.以下设a≠0.因为aa2n+a?/n2+a?2n2nnn(n'+a+n)