
5第一章函数与极限(2)y=x+lnx.(0.+)证(1)y=f(x)80.1)1设<<1.因为11f(x2)-(x)>01 - x21 -x,(1 - x )(1 - x2)所以x)>(x),即()在(-00,1)内单调增加(2)y=f(x)=x+lnx,(0,+).设0<<x2.因为12>0(2)-f(x)=x+Inx2-x-Inx=x2-x+InX1所以x)>(x),即f()在(0,+)内单调增加5.设F(x)为定义在(-1,1)内的奇函数,若(x)在(0,1)内单调增加,证明(x)在(-1.0)内也单调增加证设-1<xx0,则0-x-l由(x)是奇函数,得)-f(x)=-f(-x)+F(-x).因为F(x)在(0,1)内单调增加,所以(-)-F(-x2)>0,从而f(x2)>f(x),即(x)在(-10)内也单调增加6.设下面所考虑的函数都是定义在区间(-1,1)上的.证明:(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数证(1)设(x)J2(x)均为偶函数,则J(-x)=/(x)2(-x)=f2(x).令F(x)=f(x)+f(x),于是F(-x)=(-x)+J2(-x) =fi(x)+f2(x)=F(x),故F(x)为偶函数设gi(x),g2(x)均为奇函数,则gi(-x)=-gl(x)B2(-x)=-g2(x).令G(x)=g,(x)+g2(x),于是G(-x)=gi(-x)+g2(-x)= -gl(x)-g2(x)=-G(x),故G(x)为奇函数(2)设(x)J2(x)均为偶丽数,则(-x)=(x)J2(-x)=().令F(x)=J(x)J2(x).于是F(-x)=(-x) ·J2(-x)=fi(x)2(x)=F(x),故F(x)为偶函数设g(x),g2(x)均为奇函数,则g(-x)==gl(x),g2(-x)==g2(x).令G(x)=g(x)·g2(x).于是G(-x)=gr(-x)·g2(-x)=[-gi(α)][-g2(x))

6一、《高等数学》(第七版)上册习题全解=gi(x) - g2(x) =(x),故Gx)为偶函数设f(x)为偶函数,g(x)为奇函数,则f(x)=f(x),g(-x)=-g(x).令H(x)=f(x):g(x),于是H(-x)=f(-x)·g(-x)=f(x)[-g(x))=-f(x) g(x)=-H(x),故H(x)为奇函数,7.下列函数中哪些是偶函数,哪些是奇函数,哪些既非偶函数又非奇函数?(2) y=3x2 -x;(1) y=x2(1 -x2);(3) y=1 -x2(4)y=x(x-1)(x+1):1++2;(6) y=* +α**(5)y=sinx-cosx+l;2解(1)y=f(x)=x(1-x),因为f(-x) =(-x)[1-(-x)2] =x2(1 -x2) =f(x),所以f(x)为偶函数(2)=f(x)=3x2-x,因为f(-x)=3(-x)2-(-x)3=3x2+x3f(-x)(x),且f(-x)±-f(x),所以(x)既非偶函数又非奇函数(3) y=f(x) =1-21++2.因为( -x) =1-(-x)2_ 1-x2=(x),1 +(-x)2"1+x2所以f(x)为偶丽数(4)y=f(x)=x(x-1)(x+1),因为f(-x)=(-x)[(-x)-1[(-x)+1)= -x(x+1)(x-1) = -f(x),所以(x)为奇函数(5)y=f(x)=sinx-cosx+l,因为f(-x)=sin(-x)-cos(-x)+1=-sinx=cosx+1(x)()且(—x-)所以(x)既非偶函数又非奇函数,,因为(-)=+a(6) y=(x)= +α-*=八(x),所以(x)为偶函数228.下列各函数中哪些是周期函数?对于周期函数,指出其周期:(2)y=cos4x:(1)y=cos(x-2);(4)y=xcos x;(3)y=1+sin Tx:

7第一章函数与极限(5)y=sin?x.解(1)是周期函数,周期1=2元.(2)是周期函数,周期1=2(3)是周期函数,周期【=2.(4)不是周期函数(5)是周期函数,周期1=T.9.求下列函数的反函数:(1)y= /x+I:(2)yax+b(3) y=(4)=2sin 3x(≤x(ad-bc±0);cx+d62*(5)y=1+ln(x+2);(6) y=2+1分析函数存在反函数的前提条件为:f:D一fD)是单射.本题中所给出的各函数易证均为单射,特别(1)(4)、(5)、(6)中的函数均为单调函数,故都存在反函数解(1)由y=x+1解得x=y3-1,即反函数为y=x3-1.1-x!-解得×-,即反函数为(2)由=1+x1+y1+3(3)由y=ax+b敏解得x=岁,即反函数为=cx+dcy-acx-a1TTTY(4)由y=2sin3x≤x解得x,即反函数为arcsin66O21xaresiny=32(5)由y=1+ln(x+2)解得x=ey-1-2,即反函数为y=et-1-2.2*2,即反函数为y=log2-x(6)由y:解得x=1og212*+110.设函数(x)在数集X上有定义,试证:函数(x)在X上有界的充分必要条件是它在X上既有上界又有下界解设f(x)在X上有界,即存在M>0,使得If(x)I≤M,xeX,故-M≤f(x)≤M,xEX,即f(x)在X上有上界M下界-M.反之,设x)在X上有上界K,下界K2,即K,≤(x)≤KI,XEX

8一、《高等数学》(第七版)上册习题全解取M=max/IK,1,IK,11,则有If(x)I≤M, xEX,即fx)在X上有界.11.在下列各题中,求由所给函数构成的复合函数,并求这函数分别对应于给定自变量值x,和x2的函数值:TTT(1)y=u,u=sin x,x)6x23TT(2)y=sin u,u=2,=号.*2=年:(3)y=/u,u=1+x2,xi=1,x2=2;(4)y=e",u=x2,x =0,x,=l;(5)y=u?,u=et,x=l,x2=-1.13解(1)y=sinx,i==-2=V222=1(2) y= sin 2x,y1 =(3)y=/1+x,1=/22=/5(4) y=et,yi=l,y2=e.(5) y=e2*,y1=e?,y2=e-212.设(x)的定义域D=[01]求下列各函数的定义域:(1) f(x2) ;(2)f(sinx):(4)f(x+a)+f(x-a)(a>0).(3)f(x+a)(a>0);解1)0≤≤1=xE[-1.1](2)0≤sinx≤1=xE[2nT,(2n+1)π],nEZ(3)0≤x+a≤l=→xE[-a,1-al.r0≤x+a≤l,11时,xe[a,l-a]:当a>时,定义域为①当0a(4)20≤x-a≤113.设Ixl<1,.0.Ixl =1, g(x) =etF(x)=-1.Ix1>1,求几g(x)和g[(x)1,并作出这两个函数的图形1. x<0.0,x=0,解fg(x)J=f(e*)=-1,x>0
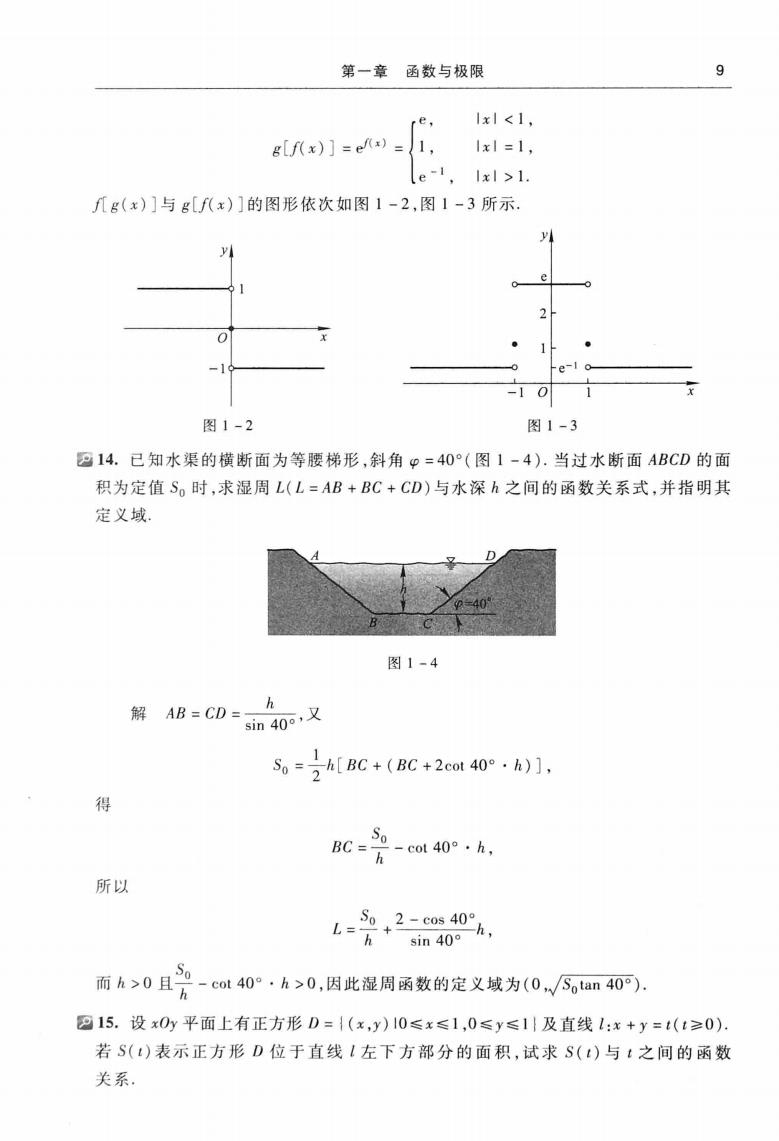
9第一章函数与极限1xl <1,re,g[(x)]=e(x)=Ixl =1,1(e-lIxI >1.几g(x)与g[f(x)的图形依次如图1-2,图1-3所示,yAYAC2x0x-10图1-2图1-314.已知水渠的横断面为等腰梯形,斜角Φ=40°(图1-4).当过水断面ABCD的面积为定值S。时,求湿周L(L=AB+BC+CD)与水深h之间的函数关系式,并指明其定义域.图1-4h解:AB=CD=sin40°,又-h[BC+(BC+2cot40°:h)],So:7得SoBC =.cot40o.h,h所以So2- cos 40°Lhsin40°So而h>0且cot40°·h>0,因此湿周函数的定义域为(0,/S。tan40°)h15.设x0y平面上有正方形D=/(x,y)10≤x≤1.0≤y≤11及直线lx+y=t(t≥0)若S)表示正方形D位于直线I左下方部分的面积,试求S()与t之间的函数关系