
(3)求和 f(5)Ax5Ax,=x i=1 i=1 0!2r0+*) a+2”-+2+ 3 涵 λ→0→n→o ca=四2ay-=+2+川》月 元→0 i=1
i i n i f x = ( ) 1 i i n i = x = 2 1 , 1 2 i n i = xi x = (3)求和 n n i n i 1 2 1 = = ( ) 2 2 2 2 3 3 1 1 1 1 2 n i i n n n = = = + + + 6 1 ( 1)(2 1) 3 + + = n n n n , 1 2 1 1 6 1 + = + n n → 0 n → x dx 1 0 2 i i n i = x = → 2 1 0 lim + = + n→ n n 1 2 1 1 6 1 lim . 3 1 = #
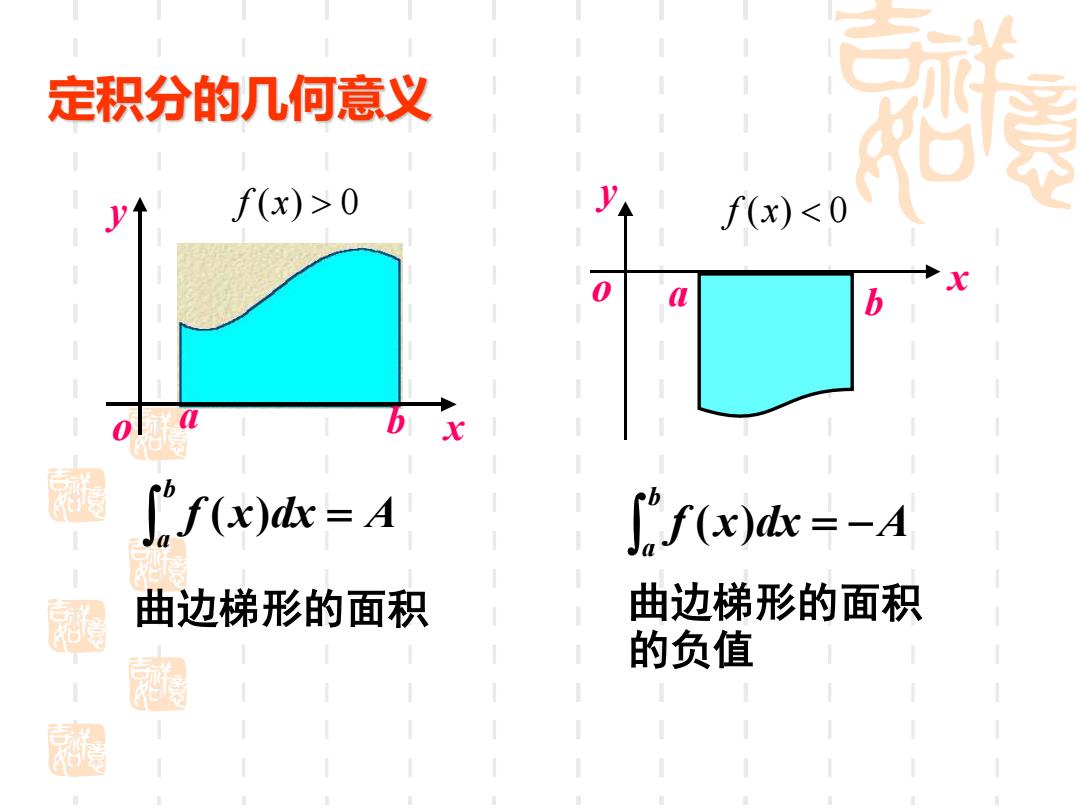
定积分的几何意义 f(x)>0 f(x)<0 0 L b X ∫fx)=A ['f(x)dx=-A 凝 曲边梯形的面积 曲边梯形的面积 的负值
f x( ) 0 = b a f (x)dx A 曲边梯形的面积 f x( ) 0 = − b a f (x)dx A 曲边梯形的面积 的负值 定积分的几何意义 a b x y o o y a b x
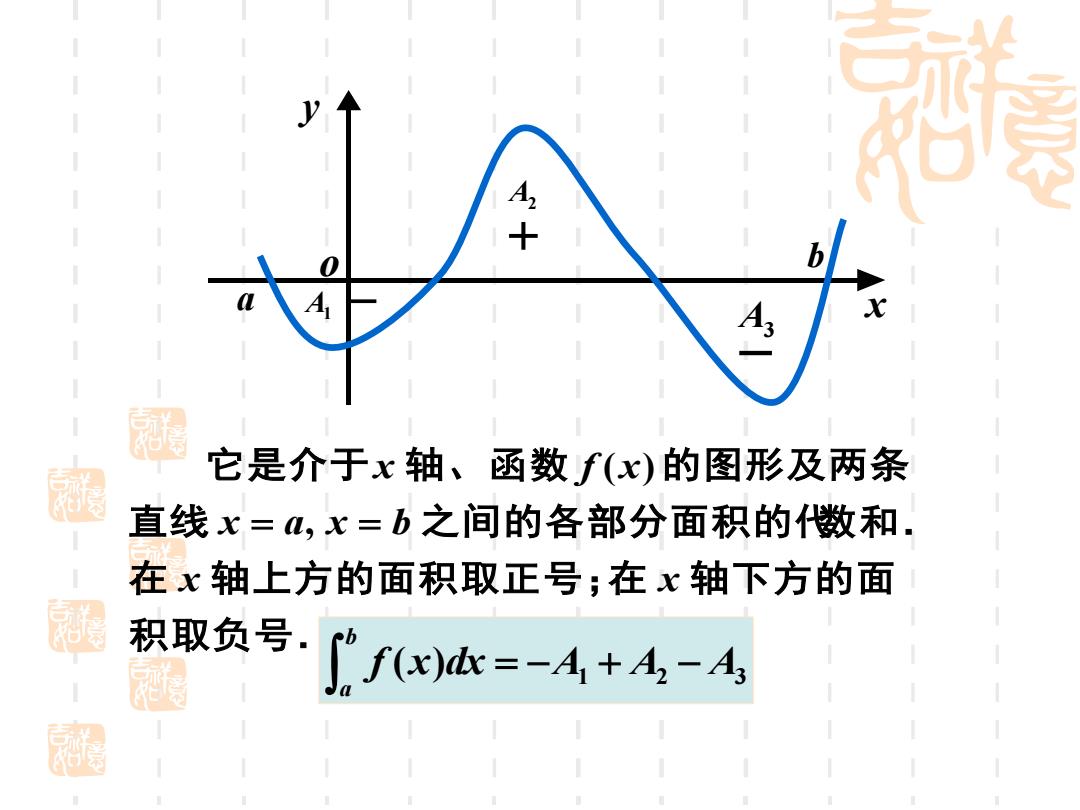
4+ 0 b A 它是介于x轴、函数f(x)的图形及两条 直线x=4,x=b之间的各部分面积的数和 在x轴上方的面积取正号;在x轴下方的面 积取负号. [f(x)d=-A+A-A
积取负号. 在 轴上方的面积取正号; 在 轴下方的面 直 线 之间的各部分面积的代数和. 它是介于 轴、函数 的图形及两条 x x x a x bx f x = , = ( ) A 1 A 2 A 3 1 2 3 f ( x )dx A A A ba = − + − − + − x y o a b

之例2利用定积分的几何意义计算定积分V1一x 解:由定积分的几何意义知,该积分值等于 曲线y=V1-x2,x轴,x=0及x=1所围 的面积(见下图) 面积值为圆的面积的 1-4 超 所以v1-d= #
例2 1 2 0 1− x dx 利用定积分的几何意义计算定积分 的面积(见下图) 曲 线y = 1− x 2 , x轴 ,x = 0及x = 1所 围 1 x y 面积值为圆的面积的 4 1 4 1 1 0 2 − = 所以 x dx o 解:由定积分的几何意义知,该积分值等于 #

对定积分的补充规定: (1)当a=b时,∫f(x)=0: (2) 当a>b时,∫f(x)dx=-∫f(x)d. 极秋秘 极泡
对定积分的补充规定: (1)当a = b时, ( ) = 0 b a f x dx ; (2)当a b时, = − a b b a f (x)dx f (x)dx