
3.2.2定积分的概念 定义3-3设fc)在[a,b]上有界,在[a,b]中任意插入若干 个分点a=x。<x,<x,<…<x<x,=b,把区间[a,b]分成 分割 个小区间,各小区间长度依次为△x,=x,-x-,i=1,2,…,n, 近似 在每个小区间上任意一点气(5∈[x,x]),作f()Ax 求和 作和式S=∑f5)△x记元=max{△x,△x2,,△x,} i=l 如果不论对[a,b]怎样的取法, 也不论在小区间[X:-1,x] 取极限 上点5气怎样的取法,若m∑f(5)A存在,则称这个 i=l 极限为函数fx)在[a,b]上的定积分。记为
定义3-3 3.2.2 定积分的概念 1 , 1, 2, , , i i i x x x i n = − = − 设 f (x) 在[a,b ]上有界,在[a,b ]中任意插入若干 ( 1 , ,) ( ) i i i i i i x x f x − 在每个小区间上任意一点 作 a x x x x x b 个分点 = 0 1 2 n−1 n = 个小区间,各小区间长度依次为 如果不论对[a,b ]怎样的取法,也不论在小区间 ,把区间[a,b]分成n max{ , , , } 1 2 n 记 = x x x 1 ( ) n i i i S f x = 作和式 = [ , ] xi−1 xi i 上点 怎样的取法,若 0 1 lim ( ) n i i i f x → = 极限为函数 f (x) 在[a,b ]上的定积分。记为 存在,则称这个 近似 求和 分割 取 极 限

积分上限 积分和式 fx)de∈lim f(5:)△x: 2→0i=1 积分下限 被积函数 被积表达式 积分变量 [a,b]→ 积分区间
= ba f(x)dx i i ni f x → = lim ( ) 1 0 被积函数 被积表达式 积分变量 [ , ] a b → 积分上限 积分下限 积分和式 积分区间

注意 (1)积分值仅与被积函数及积分区间有关, 而与积分变量的字母无关 f()dx="f()dt-f(udu 吉花 (2) 定义中区间的分法和5的取法是任意的, 溺
注意: (1) 积分值仅与被积函数及积分区间有关, b a f (x)dx = b a f (t)dt = b a f (u)du (2)定义中区间的分法和 i的取法是任意的. 而与积分变量的字母无关

曲边梯形由连续曲线y=f(x)(f(x)≥0)小、 x轴与两条直线x=a、x=b所围成 其面积A等于f(x)在区间[a,b]上的定积分: A=r(ds 设某质点作直线运动,速度y=v(t)是时间 间隔[T,T,]上t的一个连续函数,物体在这 段时间内所经过的路程
曲边梯形由连续曲线 y = f (x)( f (x) 0)、 x轴与两条直线x = a、x = b所围成. ( ) [ , ] ( ) b a A f x a b A f x dx = 其面积 等于 在区间 上的定积分: 设某质点作直线运动,速度 v = v(t)是时间 间 隔[ , ] T1 T2 上 t的一个连续函数,物体在这 段时间内所经过的路程. = 2 1 ( ) T T S v t dt
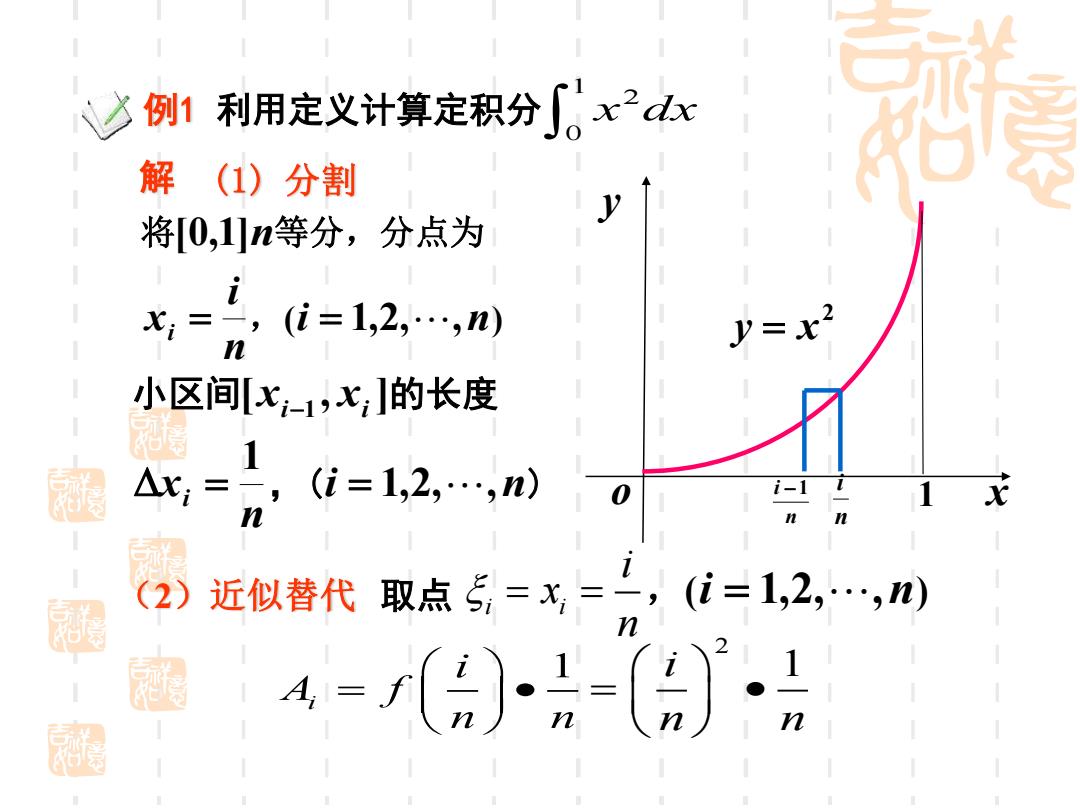
少例1利用定义计算定积分∫x2dx 解(1)分割 将[0,1]n等分,分点为 i x,=,(i=1,2,…,n) n =2 小区间x-1,x;]的长度 涵 △x,=,(i=1,2,,n) i-1 n (2) 近似替代取点=x=,i=1,2,,) 4=()气)
例1 利用定义计算定积分 1 2 0 x dx x y o 1 2 y = x n i − 1 n i 1 i i A f n n = • 2 i 1 n n = • 解 将[0,1]n等分,分点为 n i xi = ,(i = 1,2, ,n) 小区间[ , ] xi−1 xi 的长度 n xi 1 = ,(i = 1,2, ,n) (1) 分割 i i i x n (2)近似替代 取点 = = ,(i = 1,2, ,n)