第二节基坐标及其变换 一线性空间的基、向量的坐标 P(x,y,Z) (00.1) (0.1,0)1 (1,00) X 上页 返回
第二节 基 坐标及其变换 一 线性空间的基、向量的坐标 (1, 0, 0) (0, 1, 0) (0, 0, 1) X Z o P(x, y, z) A B

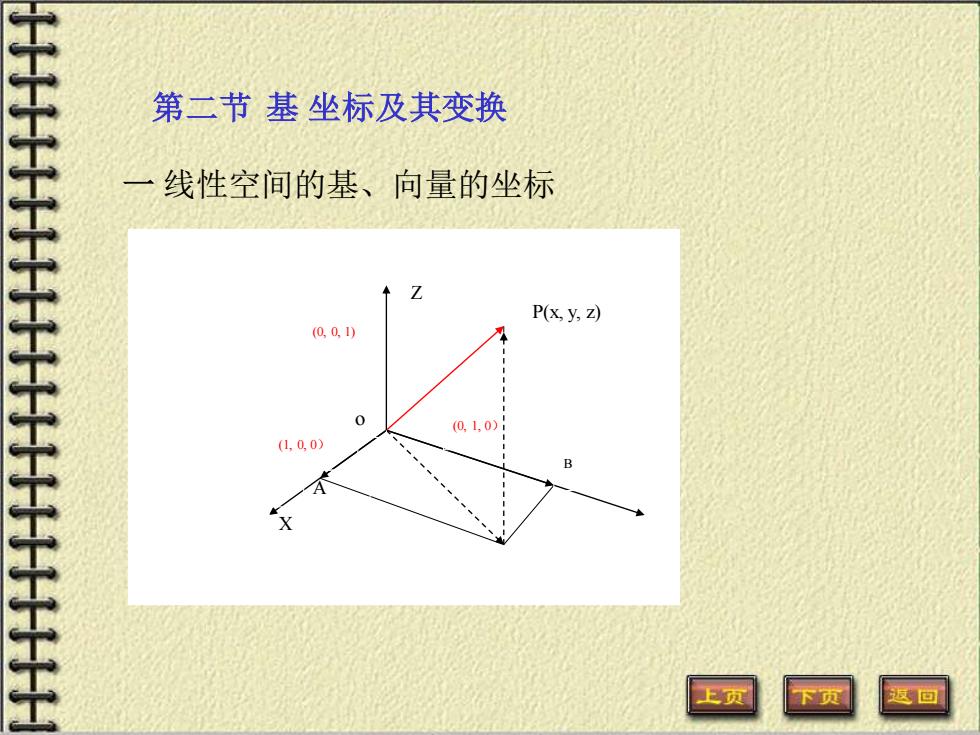
在三维实向量形成的线性空间中,常常选择一组向量: e=(1,0,0),e2=(0,1,0),e=(0,0,1)',空间中任意一 个向量可以表示成: =xe,ye,+ze,=(eee 在例4的线性空间中也存在一个向量组: 1,x,…,x”,空间中任意一个向量可以表示成 p(x)=,x,…, r" 4.… 上页
在三维实向量形成的线性空间中,常常选择一组向量: T T T e (1, 0,0) , e (0,1, 0) , e (0,0,1) 1 = 2 = 3 = ,空间中任意一 个向量可以表示成: ( ) = + + = z y x x y z xe ye ze e e e T 1 2 3 1, 2 3 ( , , ) , 在例 4 的线性空间中也存在一个向量组: 1, , , ; n x x 空间中任意一个向量可以表示成 ( ) = n n a a a p x x x 1 0 ( ) 1, ,

定义3设V是线性空间,a,C2,…,0n 是V中n个向量,如果存在一组不全为零的实数 ki k, ,kn,使得: ka,+k02+…+kan=0 则称向量组a,g,·,Q,是V中线性无 关的向量组。 显然e=(L,0,0),e2=(0,1,0),e=(0,0,1)7 线性无关; L,X,…,x线性无关。 上页 区回
定义 3 设V 是线性空间, , , , , 1 2 n 是V 中n 个向量,如果存在一 组不全为零的实数 n k , k , k 1 2 ,使得: k11 + k22 ++ k n n = 0 则称向量组 , , , , 1 2 n 是V 中线性无 关的向量组。 显 然 T T T e (1, 0,0) , e (0,1, 0) , e (0,0,1) 1 = 2 = 3 = 线性无关; 1, , , ; n x x 线性无关

定义4设V是线性空间,Q,o2,, c,是V中n 个向量 (1),,,an,线性无关: (2)V中任意一个向量Q可以表示成 01,02, ,αn,的,线性组合,既是: =x0+x2+…+x,n=(a,2,…, 称0, 02,…, n,是线性空间V的一个基(底),其 个数n称为V的维数,记为 dimV=n X=x,x2,,x,)称为向量a在这个基下的坐标。 注意:1.在线性空间中基不唯一; 2.在同一个基下,向量和它的坐标一一对应
定 义 4 设V 是线性空间, , , , , 1 2 n 是V 中n 个向量 (1) , , , , 1 2 n 线性无关; ( 2 ) V 中任意一个向量 可 以 表 示 成 , , , , 1 2 n 的 , 线 性 组 合 , 既 是 : ( ) = + + + = n n n n x x x x x x 2 1 1 1 2 1 2 , , , 称 , , , , 1 2 n 是 线性空间V 的一个基(底),其 个 数 n 称 为 V 的 维 数 , 记 为 dimV = n , ( ) T n X x , x , , x = 1 2 称为向量在这个基下的坐标。 注意: 1. 在线性空间中基不唯一; 2. 在同一个基下,向量和它的坐标一一对应

例在3维实向量空间R中选择两个基 (1)e,=(1,0,0)',e2=(0,1,0),e=(0,0,1) (2)e=(1,0,0),e2=(L,1,0)',e=(1,1,1) 求向量α=(10,-2,3)'在两个基下的坐标。 解求坐标方程为: 0 xe1+xe2+x,e3=a→x 解得坐标(x,x2,x)'=(10, -2, 3) ye1+ye2+y,e3=a→x 解得坐标 (y,y2,y)y=12,-5, 3 回
例 在 3 维实向量空间 3 R 中选择两个基 (1) T T T e (1, 0,0) , e (0,1, 0) , e (0,0,1) 1 = 2 = 3 = (2) T T T e (1,0,0) , e (1,1,0) , e (1,1,1) ' 3 ' 2 ' 1 = = = 求向量 T = (10, − 2, 3) 在两个基下的坐标。 解 求坐标方程为: = − + + + + = 3 2 10 1 0 0 0 1 0 0 0 1 1 1 2 2 3 3 1 2 3 x e x e x e x x x 解得坐标 ( ) ( ) T T x1 , x2 , x3 = 10, − 2, 3 。 = − + + + + = 3 2 10 1 1 1 0 1 1 0 0 1 ' ' ' 1 1 2 2 3 3 1 2 3 y e y e y e x x x 解得坐标 ( ) ( ) T T y1 , y2 , y3 = 12, − 5, 3