导读 在学习二重积分的时候,注意和定积分的相关概念之间的区别 与联系.与定积分类似,二重积分的概念也是从实践中抽象出来的, 它是定积分的推广,其中的数学思想与定积分一样,也是一种“和式 的极限”.所不同的是:定积分的被积函数是一元函数,积分范围是 一个区间;而二重积分的被积函数是二元函数,积分范围是平面上的 一个区域.它们之间存在着密切的联系,二重积分可以通过定积分来 计算
导 读 6 在学习二重积分的时候,注意和定积分的相关概念之间的区别 与联系. 与定积分类似,二重积分的概念也是从实践中抽象出来的, 它是定积分的推广,其中的数学思想与定积分一样,也是一种“和式 的极限”. 所不同的是:定积分的被积函数是一元函数,积分范围是 一个区间;而二重积分的被积函数是二元函数,积分范围是平面上的 一个区域. 它们之间存在着密切的联系,二重积分可以通过定积分来 计算

一、二重积分的概念和性质 第七章多元函数积分学 第一节二重积分的概念、计算及应用 一、 二重积分的概念和性质 二、直角坐标系下二重积分的计算 三、极坐标系下二重积分的计算 四、二重积分的还元法 五、二重积分的应用
7 第七章 多元函数积分学 四、二重积分的还元法 一、二重积分的概念和性质 二、直角坐标系下二重积分的计算 第一节 二重积分的概念、计算及应用 一、二重积分的概念和性质 五、二重积分的应用 三、极坐标系下二重积分的计算
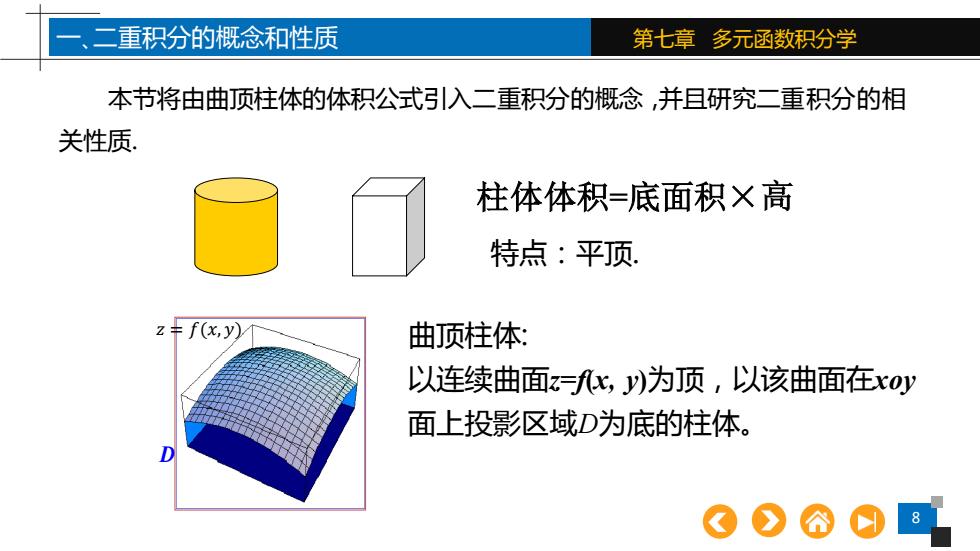
二重积分的概念和性质 第七章多元函数积分学 本节将由曲顶柱体的体积公式引入二重积分的概念,并且研究二重积分的相 关性质, 柱体体积=底面积×高 特点:平顶 z=f(x,y) 曲顶柱体: 以连续曲面z=fx,y)为顶,以该曲面在x0y 面上投影区域D为底的柱体
8 第七章 多元函数积分学 柱体体积=底面积×高 特点:平顶. 一、二重积分的概念和性质 本节将由曲顶柱体的体积公式引入二重积分的概念,并且研究二重积分的相 关性质. 𝑧 = 𝑓(𝑥, 𝑦) D 曲顶柱体: 以连续曲面z=f(x, y)为顶,以该曲面在xoy 面上投影区域D为底的柱体

第七章多元函数积分学 1.曲顶柱体的体积 类似于曲边梯形面积的求法我们采取“分割”、 AZ “近似”、“求和”、“取极限”的步骤来求曲顶柱 z=f(xy) 体的体积 图7-3 (1)分割△D,△D2,.△Dn△g1,△c2,△0m f(xy) (2)近似 任取一点(x,)≈f(x,y)△o (3)求和 ∑f,yWAa i= (4)取极限 ∑f,y)△g
9 第七章 多元函数积分学 1. 曲顶柱体的体积 类似于曲边梯形面积的求法,我们采取“分割”、 “近似”、“求和”、“取极限”的步骤来求曲顶柱 体的体积. D f (xi,yi) z=f (x ,y ) x O y (x i ,y i ) ▲▲▲ 图 7 - 3 (1)分割 (2)近似 (3)求和 (4)取极限

1、曲顶主体的体积 第七章多元函数积分学 上面的问题把所求量归结为和式的极限.由于在物理、力学、几何和工程中 技术中,许多的物理量和几何量都可以用这样的和式的极限来表示,所以有必 要研究这种和式的极限的一般形式,我们从上述从表达式中抽象出下面的二重积 分的定义
10 第七章 多元函数积分学 上面的问题把所求量归结为和式的极限. 1、曲顶主体的体积 所以有必 要研究这种和式的极限的一般形式,我们从上述从表达式中抽象出下面的二重积 分的定义. 由于在物理、力学、几何和工程中 技术中,许多的物理量和几何量都可以用这样的和式的极限来表示