3位置矢量与运动方程 位置矢量(位矢) P(xy,) 从坐标原点o出发,指向质 点所在位置P的一有向线段 位矢用坐标值表示为: 下=xi+y功+zk 位矢的大小为: r=vx2+x2+22 位矢的方向: c0sa=cos月=cos7=月
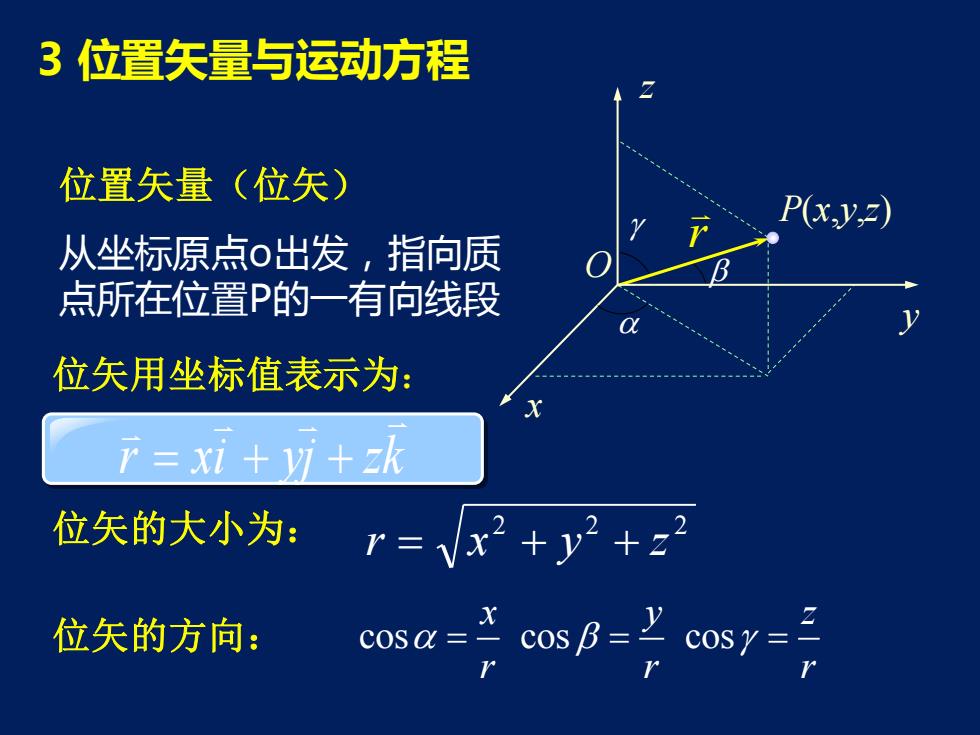
3 位置矢量与运动方程 位置矢量(位矢) 从坐标原点o出发,指向质 点所在位置P的一有向线段 位矢用坐标值表示为: r xi yj zk = + + 位矢的大小为: 2 2 2 r = x + y + z 位矢的方向: cos cos cos x y z r r r = = = P(x,y,z) r z y x O

运动方程 r =x(t)i +y(t)j+z(t)k 参数形式 x=x(t) y=y(t) 轨道方程 z=z(t) F(x,y,z)=0
r x t i y t j z t k = ( ) + ( ) + ( ) 运动方程 参数形式 ( ) ( ) ( ) z z t y y t x x t = = = 轨道方程 F(x, y,z) = 0
4位移 设质点作曲线运动 t时刻位于A点,位矢下4 t什△时刻位于B点,位矢B 在△t时间内,位矢的变化量(即A到B 的有向线段)称为位移。 △F=TB-FA=AB
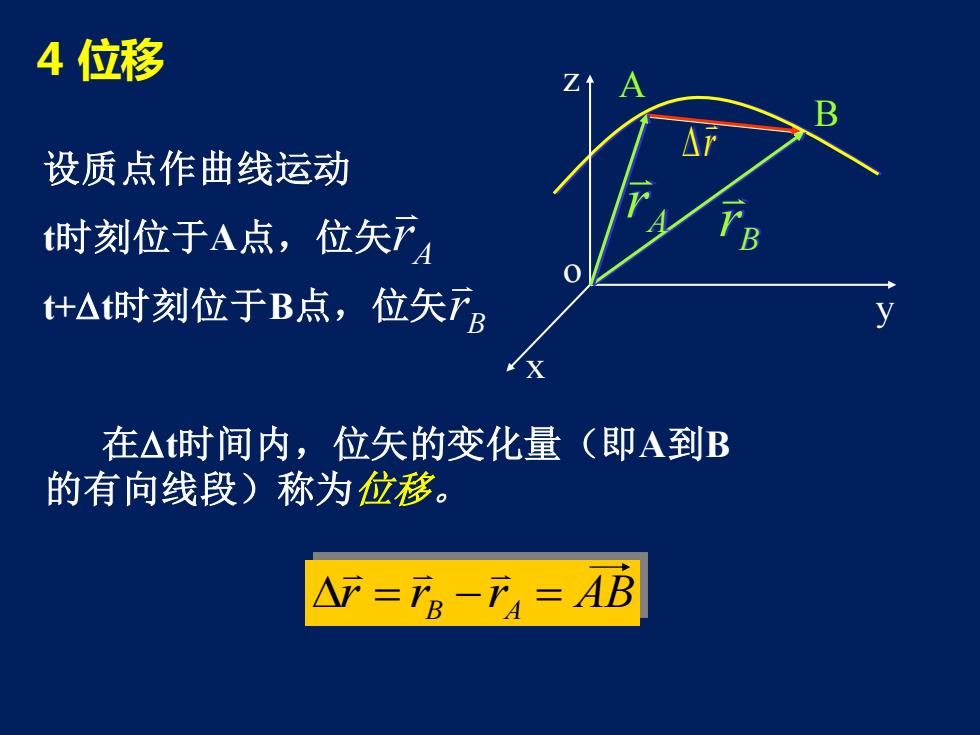
4 位移 设质点作曲线运动 t时刻位于A点,位矢 t+t时刻位于B点,位矢 A r B r 在t时间内,位矢的变化量(即A到B 的有向线段)称为位移。 r z y x o B r B A r A r = rB −rA = AB
5速度 速度是反映质点运动的快慢和方向的物理量 定义:单位时间内质点所发生的位移 (1)平均速度 △7 (m/s) △t (2) 瞬时速度 △rd -l9¥h ms) 速度的方向为轨道上质点所在处的切线方向
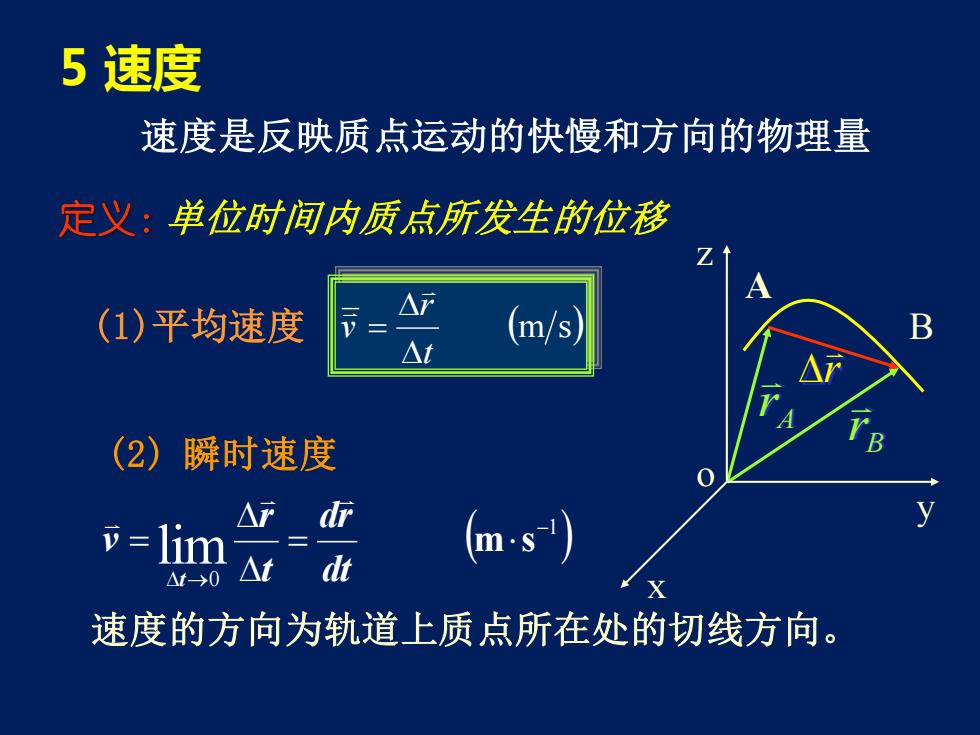
5 速度 速度是反映质点运动的快慢和方向的物理量 定义:单位时间内质点所发生的位移 (1)平均速度 B A o z y x A r B r r (2) 瞬时速度 ( ) 1 0 lim − → = = m s dt dr t r v t 速度的方向为轨道上质点所在处的切线方向。 (m s) t r v =

V=vi+r,j+vk v==++ △s ds (3)速率 V= lim △1→0 △t dt 一般情况:≠△s因此同≠ 当△-→0时:△→=则=y
v v i v j v k x y z = + + 2 2 2 x y z v = v = v + v + v (3) 速率 dt ds ts v t = = → lim0 一般情况: r s v v 因此 当 t → 0时: r → dr = ds v = v 则 s r B A