
不定积分 第三章一元函数积分学及其应用 定义2 在区间I上,函数f(x)的带有任意常数项的原函数称 ◇ 为f(x)在区间I上的不定积分,记作[fxHx,即 不定积分的概念 ∫fxHr=Fx)+C 其中,符号[称为积分号,称f(x)为被积函数,f(x)dx称为被积表达 式,x称为积分变量,F(x)是f(x)的一个原函数
6 第三章 一元函数积分学及其应用 定义2 f (x) x = F(x) + C d . 其 中, 符 号 称 为积分号, 称 f (x)为被积函数, f x x ( )d 称 为被积表达 式, x称为积分变量, F(x)是 f (x)的一个原函数. 不定积分的概念 二、不定积分 在区间 I 上, 函 数 f x( ) 的带有任意常数项的原函数称 为 f x( ) 在区间 I 上的不定积分, 记作 f (x)dx , 即

不定积分 第三章一元函数积分学及其应用 由定义知,求函数f)的不定积分,就是求fx)的全体原函数在f(x)dx 中, 积分号∫表示对函数f)施行求原函数的运算,故求 不定积分的运算实质上就是求导求微分)运算的逆运算
7 第三章 一元函数积分学及其应用 由定义知, 求函数 f (x) 的不定积分, 就是求 f (x) 的全体原函数.在 f x x ( )d 中, 积分号 表示对函数 f (x) 施行求原函数的运算, 故求 不定积分的运算实质上就是求导(求微分)运算的逆运算. 二、不定积分

二 不定积分 第三章一元函数积分学及其应用 按照定义,一个函数的原函数或不定积分都有相应的定义区间.为了简便起 见,如无特别的说明,今后就不再注明 例1 设f)和fx)均连续,问:d(fx)dr)与f(xh是否相等? 解 不相等 设F'(x)=f(x),则 &a品r+O-F)+0= 而由不定积分定义/x)d=f)+c,知&fx)d)+fx) 8
8 第三章 一元函数积分学及其应用 例1 设 f (x) 和 f x'( ) 均连续, 问: ( ) d ( )d d f x x x 与 f x x ( )d 是否相等? 解 不相等. 设 F(x) = f (x),则 ( ) d ( )d d f x x x d ( ( ) ) d F x C x = + = F(x) + 0 = f (x). 而由不定积分定义 f x x ( )d = f (x) + C , 知 ( ) d ( )d d f x x x f x x ( )d . 二、不定积分 按照定义, 一个函数的原函数或不定积分都有相应的定义区间. 为了简便起 见, 如无特别的说明, 今后就不再注明
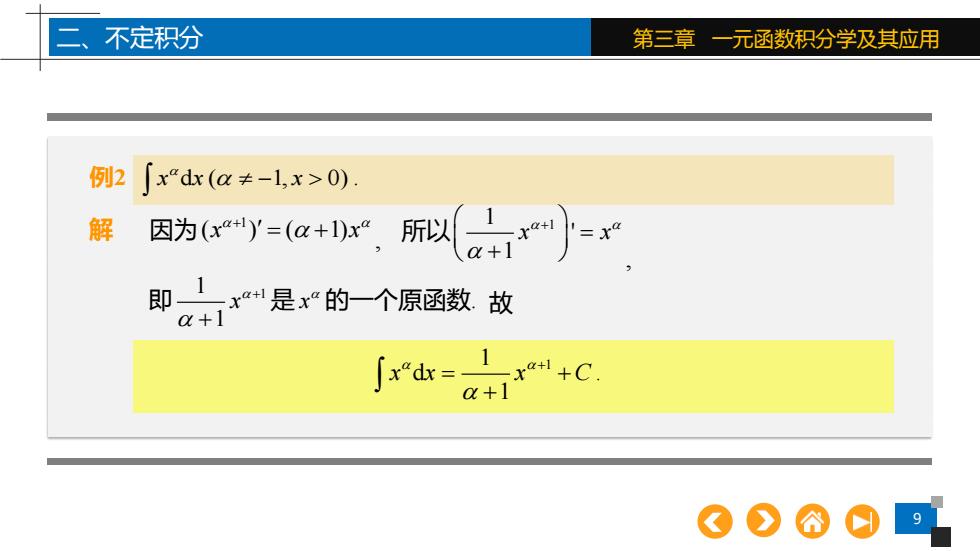
不定积分 第三章一元函数积分学及其应用 例2「x“dr(a≠-l,x>0). 解 因为(axa+)y=(a+1)x所以 即是F的个原函数故 ∫rd=1x+C +1
9 第三章 一元函数积分学及其应用 解 因为 1 ( ) ( 1) x x + = + , 二、不定积分 1 1 d 1 x x x C + = + + . 例2 x x x d ( 1, 0) − . 所以 1 1 ' 1 x x + = + , 即 1 1 1 x + + 是 x 的一个原函数. 故

二 不定积分 第三章一元函数积分学及其应用 例3 求∫dx(∫xd) 解 当x>0时,mxy=1 当x<0时即-x>0时m(-x=1(←1)= 故nx为二在(0,+w)上的一个原函数,ln(-x)为二在(-o,0)上的一个原函 数 故当x≠0时,nx为二的一个原函数,从而 ∫片dr=ln+C(x≠o 10
10 第三章 一元函数积分学及其应用 例3 求 1 dx x ( 1 x xd − ). 解 当 x 0时, 1 (ln ) x x = ; 当 x 0 时, 即− x 0时, 1 1 [ln( )] ( 1) x x x − = − = − . 故 ln x 为 1 x 在 (0, ) + 上的一个原函数, ln( ) −x 为 1 x 在 ( ,0) − 上的一个原函 数. 故当 x 0时, ln x 为 1 x 的一个原函数, 从而 1 d ln ( 0) x x C x x = + . 二、不定积分