
第二章第四节矩阵的秩及其求法11一、矩阵秩的概念招矩阵秩的求法-社满秩矩阵三-0
1 一、矩阵秩的概念 二、矩阵秩的求法 第四节 矩阵的秩及其求法 第二章 三、满秩矩阵

1矩阵的秩的概念1111/1.k阶子式1设A=定义1在A中任取k行k列交叉处元素按原相对位置组成的 k(1<k≤min (m,n)11阶行列式,称为A的一个k阶子式-1怡索111福111一一11111111-1111福酒11E1.1I11111/110211/1
2 1. k 阶子式 定义1 设 ( ) m n A aij = 在A中任取k 行k 列交叉 k (1 k min m,n) 阶行列式,称为A的一个k 阶子式。 处元素按原相对位置组成的 一、矩阵的秩的概念
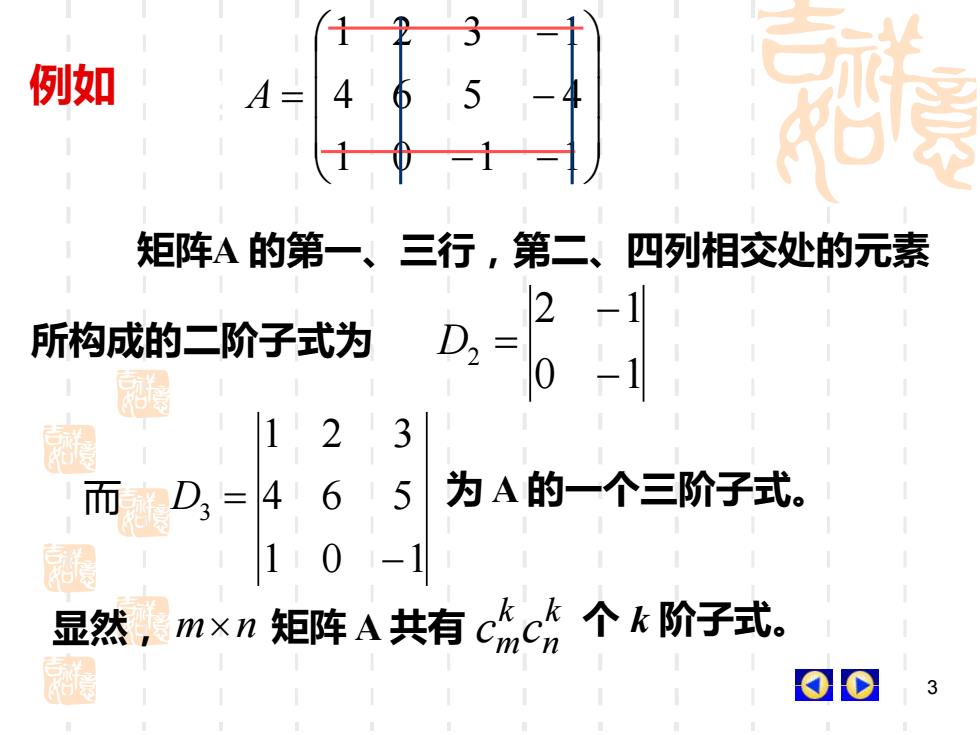
例如5AA11矩阵A 的第一、三行,第二、四列相交处的元素2-1D,所构成的二阶子式为011235为 A的一个三阶子式。64而D三01kk个k阶子式。显然矩阵A共有mxnmcn103
3 设 − − − − = 1 0 1 1 4 6 5 4 1 2 3 1 例如 A , 矩阵A 的第一、三行,第二、四列相交处的元素 所构成的二阶子式为 0 1 2 1 2 − − D = 而 1 0 1 4 6 5 1 2 3 3 − D = 为 A 的一个三阶子式。 显然, mn 矩阵 A 共有 k n k cmc 个 k 阶子式

1111112. 矩阵的秩/有r阶子式不为0,任何r+1阶定义2设A=(a.mx子式(如果存在的话)全为0,称r为矩阵A的秩,1记作R(A)或秩(A)。111/11111?111111-11111111111111福1111I?1111I111111111104111111
4 2. 矩阵的秩 ( ) m n A aij 设 = ,有r 阶子式不为0,任何r+1阶 记作R(A)或秩(A)。 子式(如果存在的话)全为0 , 定义2 称r为矩阵A的秩

吉祥规定:零矩阵的秩为0.1注意:(1)如R(A)=r,则A中至少有一个r阶子式D.≠0,所有r+1阶子式为0,且更高阶子式均为 0,r是 A 中非零的子式的最高阶数1(2) 由行列式的性质,R(A)=R(A').(3) R(A) ≤m, R(A) <n, 0 <R(A) <min ( m, n }1(4)如果Anxn,且|A|±0,则R(A)=n. i反之,如R(A)=n,则A≠0.香因此,方阵A可逆的充分必要条件是R(A)=nO5R
5 规定: 零矩阵的秩为 0 . 注意:(1) 如 R ( A ) = r,则 A 中至少有一个 r 阶子 式 0 , D r 所有 r + 1 阶子式为 0,且更高阶 子式均为 0,r 是 A 中非零的子式的最高阶数. (2) 由行列式的性质, ( ) ( ) . T R A R A = (3) R(A) ≤m, R(A) ≤n, 0 ≤R(A) ≤min { m , n } . (4) 如果 An×n , 且 A 0 , 则 R ( A ) = n . 反之,如 R ( A ) = n ,则 A 0 . 因此,方阵 A 可逆的充分必要条件是 R ( A ) = n