
B=wc2-wcl;2)将指标转换为归一化模拟低通频率指标norm_wr1=((wr1^2)-(w0×2)/(B*wr1);norm_wr2=(((wr2^2)-(w0^2))/(B*wr2));norm_wc1=((we1^2)-(w0^2)/(B*wecl);norm_wc2=((wc2^2)-(w0^2)/(B*wc2);3)设计归一化模拟低通滤波器确定归一化截频if(abs(norm_wr1)-abs(norm_wr2))>0norm_wr=abs(norm_wr2);elsenorm_wr=abs(norm_wr1),endnorm_wc=1;确定归一化模拟低通滤波器阶数N=buttord(norm_wc,norm_wr,Apmax ,Armin,'s);设计归一化模拟低通滤波器[b_LP,a_LP]-butter(N,norm_wc,'s);4)把归一化模拟低通滤波器转换为模拟带通滤波器[b_BP,a_BP]-lp2bp(b_LP,a_LP,w0,B);5)利用脉冲响应不变法把模拟滤波器转换为数字滤波器Fs=1/T,[b,a]=impinvar(b_BP,a_BP,Fs);w=linspace(0,2*pi,500),h=freqz(b,a, w);
B=wc2-wc1; 2) 将指标转换为归一化模拟低通频率指标 norm_wr1=(((wr1^2)-(w0^2))/(B*wr1)); norm_wr2=(((wr2^2)-(w0^2))/(B*wr2)); norm_wc1=(((wc1^2)-(w0^2))/(B*wc1)); norm_wc2=(((wc2^2)-(w0^2))/(B*wc2)); 3) 设计归一化模拟低通滤波器确定归一化截频 if (abs(norm_wr1)-abs(norm_wr2))>0 norm_wr=abs(norm_wr2); else norm_wr=abs(norm_wr1); end norm_wc=1; 确定归一化模拟低通滤波器阶数 N=buttord(norm_wc,norm_wr,Apmax ,Armin,'s'); 设计归一化模拟低通滤波器 [b_LP,a_LP]=butter(N,norm_wc,'s'); 4) 把归一化模拟低通滤波器转换为模拟带通滤波器 [b_BP,a_BP]=lp2bp(b_LP,a_LP,w0, B); 5) 利用脉冲响应不变法把模拟滤波器转换为数字滤波器 Fs=1/T; [b,a]=impinvar(b_BP,a_BP,Fs); w=linspace(0,2*pi,500); h=freqz(b,a,w);
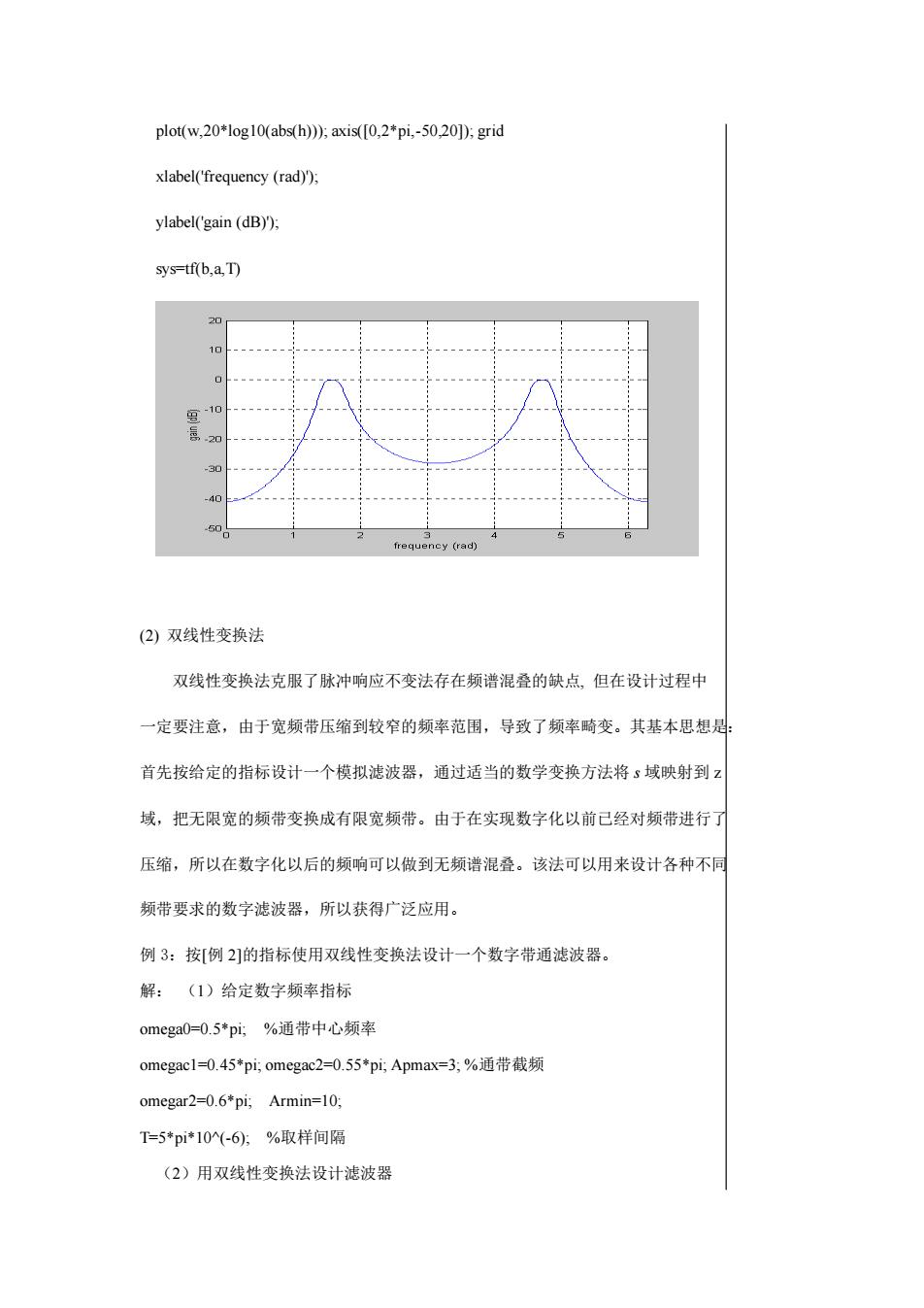
plot(w,20*log10(abs(h)); axis([0,2*pi,-50,20), gridxlabel(frequency (rad));ylabel(gain (dB));sys=tf(b,a, T)n8uletfrequency(rad)(2)双线性变换法双线性变换法克服了脉冲响应不变法存在频谱混叠的缺点,但在设计过程中一定要注意,由于宽频带压缩到较窄的频率范围,导致了频率畸变。其基本思想是首先按给定的指标设计一个模拟滤波器,通过适当的数学变换方法将s域映射到乙域,把无限宽的频带变换成有限宽频带。由于在实现数字化以前已经对频带进行了压缩,所以在数字化以后的频响可以做到无频谱混叠。该法可以用来设计各种不同频带要求的数字滤波器,所以获得广泛应用。例3:按[例21的指标使用双线性变换法设计个数字带通滤波器。解:(1)给定数字频率指标omega0=0.5*pi;%通带中心频率omegacl=0.45*pi;omegac2=0.55*pi,Apmax=3;%通带截频omegar2=0.6*pi,Armin=10,T=5*pi*10(-6);%取样间隔(2)用双线性变换法设计滤波器
plot(w,20*log10(abs(h))); axis([0,2*pi,-50,20]); grid xlabel('frequency (rad)'); ylabel('gain (dB)'); sys=tf(b,a,T) (2) 双线性变换法 双线性变换法克服了脉冲响应不变法存在频谱混叠的缺点, 但在设计过程中 一定要注意,由于宽频带压缩到较窄的频率范围,导致了频率畸变。其基本思想是: 首先按给定的指标设计一个模拟滤波器,通过适当的数学变换方法将 s 域映射到 z 域,把无限宽的频带变换成有限宽频带。由于在实现数字化以前已经对频带进行了 压缩,所以在数字化以后的频响可以做到无频谱混叠。该法可以用来设计各种不同 频带要求的数字滤波器,所以获得广泛应用。 例 3:按[例 2]的指标使用双线性变换法设计一个数字带通滤波器。 解: (1)给定数字频率指标 omega0=0.5*pi; %通带中心频率 omegac1=0.45*pi; omegac2=0.55*pi; Apmax=3; %通带截频 omegar2=0.6*pi; Armin=10; T=5*pi*10^(-6); %取样间隔 (2)用双线性变换法设计滤波器

1)按给定数字频率求得相应的模拟角频率:频率预畸变omegar1=0mega0-(omegar2 - omega0);wc1=(2/T)*tan(omegac1/2);wc2=(2/T)*tan(omegac2/2)wr1=(2/T)*tan(omegar1/2);wr2=(2/T)*tan(omegar2/2)w0=(2/T)*tan(omega0/2);B=wc2-wcl;2)将指标转换为归一化模拟低通频率指标norm_wr1=((wr1^2)-(w0×2)/(B*wr1);norm_wr2=((wr2^2)-(w0^2)/(B*wr2);norm_wcl=((we1^2)-(w0^2)/(B*wc1):norm_wc2=((wc2^2)-(wo^2)/(B*wc2);3)设计归一化模拟低通滤波器确定归一化截频:if(abs(norm_wr1)-abs(norm_wr2)>0norm_wr=abs(norm_wr2);elsenorm_wr=abs(norm_wr1);endnorm_wc=1;确定归一化模拟低通滤波器阶数:N=buttord(norm_wc,norm_wr,Apmax,Amin,'s)设计归一化模拟低通滤波器:[b_LP,a_ LP]=butter(N,norm_wc,'s);4)把归一化模拟低通滤波器转换为模拟带通滤波器[b_BP,a_BP]=lp2bp(b_LP,a_LP,w0,B);5)转换为数字滤波器Fs=1/T,[b,a]=bilinear(b_BP,a_BP,Fs);w=linspace(0,2*pi,500);h=freqz(b,a,w);plot(w,20*log10(abs(h); axis([0,2*pi,-120,20); grid
1) 按给定数字频率求得相应的模拟角频率:频率预畸变 omegar1=omega0-(omegar2 - omega0); wc1=(2/T)*tan(omegac1/2); wc2=(2/T)*tan(omegac2/2); wr1=(2/T)*tan(omegar1/2); wr2=(2/T)*tan(omegar2/2); w0=(2/T)*tan(omega0/2); B=wc2-wc1; 2) 将指标转换为归一化模拟低通频率指标 norm_wr1=(((wr1^2)-(w0^2))/(B*wr1)); norm_wr2=(((wr2^2)-(w0^2))/(B*wr2)); norm_wc1=(((wc1^2)-(w0^2))/(B*wc1)); norm_wc2=(((wc2^2)-(w0^2))/(B*wc2)); 3) 设计归一化模拟低通滤波器确定归一化截频: if (abs(norm_wr1)-abs(norm_wr2))>0 norm_wr=abs(norm_wr2); else norm_wr=abs(norm_wr1); end norm_wc=1; 确定归一化模拟低通滤波器阶数: N=buttord(norm_wc,norm_wr,Apmax,Armin,'s'); 设计归一化模拟低通滤波器: [b_LP,a_LP]=butter(N,norm_wc,'s'); 4) 把归一化模拟低通滤波器转换为模拟带通滤波器 [b_BP,a_BP]=lp2bp(b_LP,a_LP,w0,B); 5) 转换为数字滤波器 Fs=1/T; [b,a]=bilinear(b_BP,a_BP,Fs); w=linspace(0,2*pi,500); h=freqz(b,a,w); plot(w,20*log10(abs(h))); axis([0,2*pi,-120,20]); grid