
信号的抽样·连续信号频谱X(iの)与抽样信号频谱X(ej2)的关系·时域抽样定理·抗混叠滤波·信号的重建通信与电子信息系
通信与电子信息系 •连续信号频谱X(jw)与抽样信号频谱X(ejW ) 的关系 •时域抽样定理 •抗混叠滤波 •信号的重建 信号的抽样
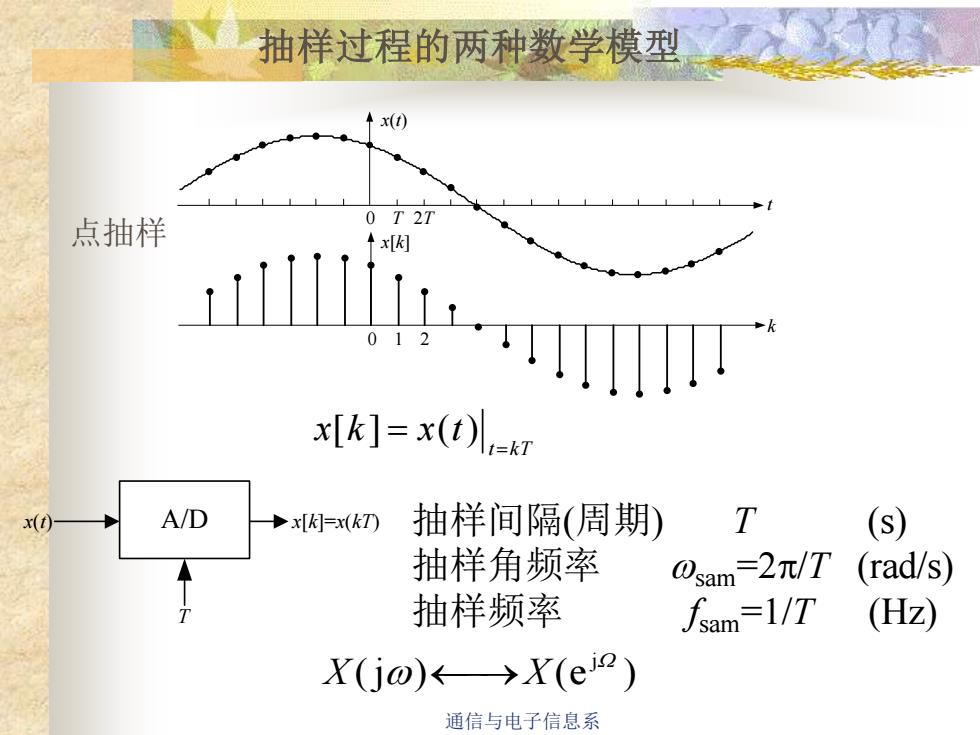
抽样过程的两种数学模型x(0)T 2T0点抽样x[K]012x[k] = x(t)]t=k1TA/D抽样间隔(周期)(s)★x[K]=x(kT)x(t)抽样角频率0sam=2元/T(rad/s)抽样频率(Hz)Jsam=1/TX(jo)<→>X(ej?)通信与电子信息系
通信与电子信息系 抽样过程的两种数学模型 x(t) t 0 T 2T x[k] k 0 1 2 t k T x k x t = [ ] = ( ) 点抽样 x(t) A/D x[k]=x(kT) T 抽样间隔(周期) T (s) 抽样角频率 wsam=2p/T (rad/s) 抽样频率 f sam=1/T (Hz) (j ) (e ) jW X w ⎯→X
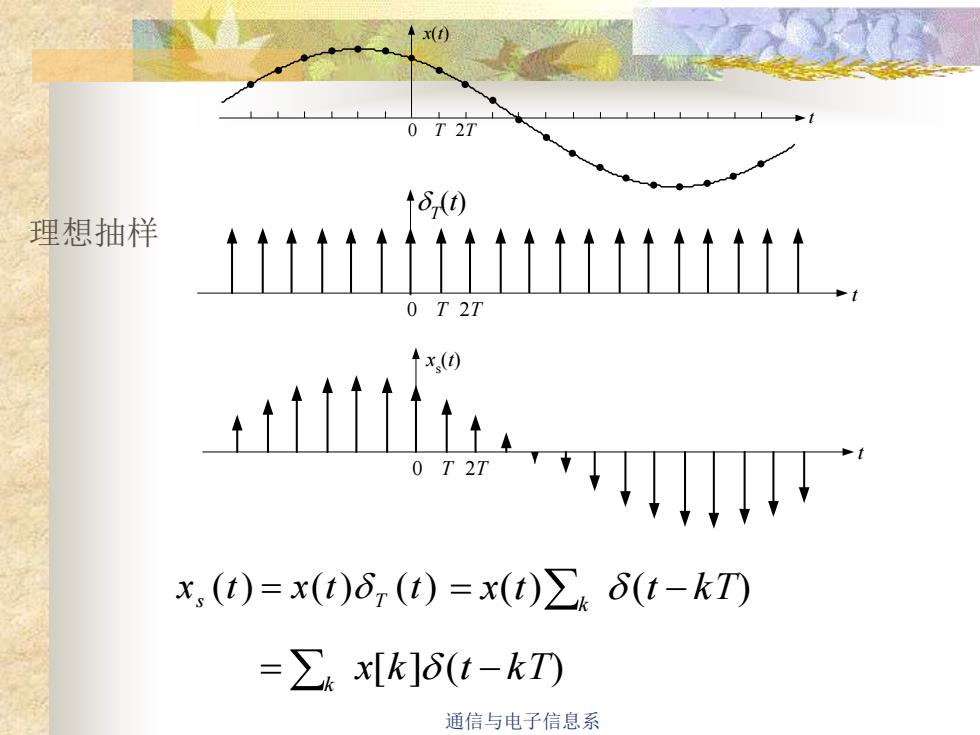
x(t)T2T08,(t)理想抽样0T 2Tx(t)T 2T0x,(t)= x(t)r(t) =x(t)Zk S(t -kT)=, x[k]S(t-kT)通信与电子信息系
通信与电子信息系 x(t) t 0 T 2T T(t) t 0 T 2T xs (t) t 0 T 2T 理想抽样 x (t) x(t) (t) s = T x[k] (t k T) k = − x(t) (t k T) k = −

的性质Sr(t)= Z S(t-nT)n=-00S(t)的Fourier变换NS. (t)<→sarS(-nOsamsamnS(t)与信号周期化的关系:x(t)*S(t)= Z x(t)*S(t-nT)n=-00Z x(t-nT)=x(t)n=-00通信与电子信息系
通信与电子信息系 T (t)的性质 T (t)的Fourier变换: ( ) ( ) wsam w nwsam t n T ⎯→ − T (t)与信号周期化的关系: x(t) (t nT) n − =− x(t) T (t) = x(t nT) x (t) T n = − = =− (t) (t nT) n T = − =−
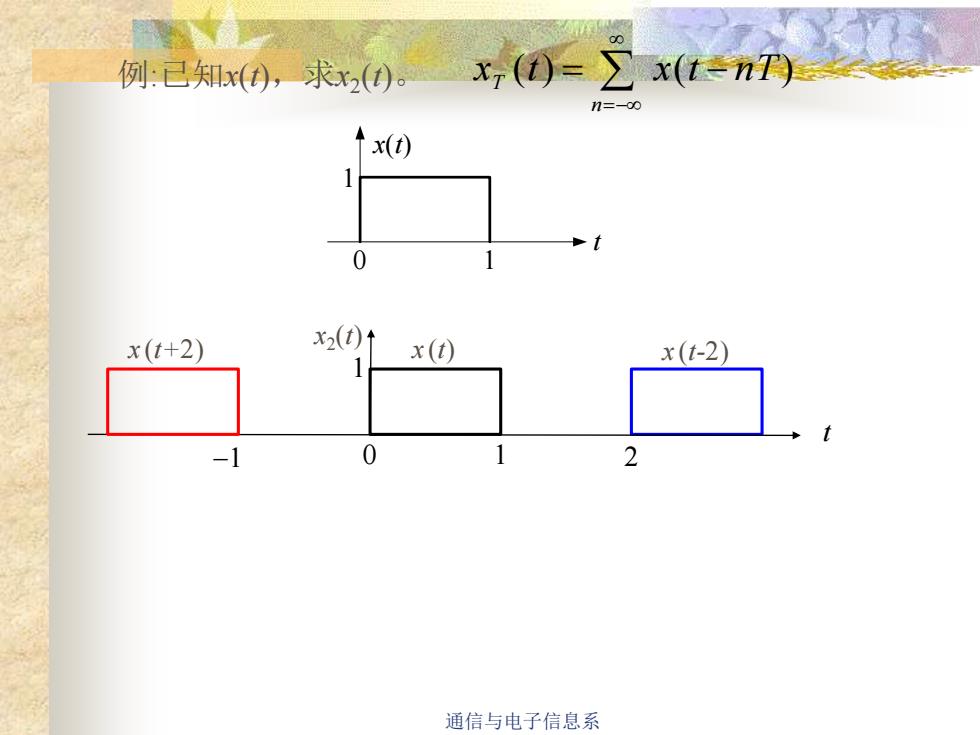
x(t)=Ex(t-nT)例已知x(t),求x()En=-00↑ x(t)01x2(t)x(t)x(t+2)x(t-2)012-1通信与电子信息系
通信与电子信息系 例:已知x(t),求x2 (t)。 x(t) t 0 1 1 2 t x2 (t) x (t+2) x (t) x (t-2) −1 0 1 1 x (t) x(t nT) n T = − =−