
极小范数最小二乘解 定理2 ·设A∈Cmxa,b∈Cm ·则x=A+b是方程Ax=b的极小范数最小二乘解 ·反之,若存在 。若对于所有X∈Cnxm b∈Cm ·x=Xb均成为方程Ax=b的极小范数最小二乘解 ·则X=A+ 冬定理3 ·矩阵方程AXB=D极小范数最小二乘解唯一 ·且为X=A+DB+ lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 6 极小范数最小二乘解 定理2 设 • 则x=A+b是方程Ax=b的极小范数最小二乘解 反之,若存在 • 若对于所有 • x=Xb均成为方程Ax=b的极小范数最小二乘解 • 则X=A+ 定理3 矩阵方程AXB=D极小范数最小二乘解唯一 且为 mn m A C ,b C × ∈ ∈ n m X C × ∈ m b C∈

第20讲全面最小二乘法 冬法向回归 冬全面最小二乘法 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 7 第20讲 全面最小二乘法 法向回归 全面最小二乘法

法向回归 再看实验数据处理 ·一组测量数据(t,s),欲拟和直线s=ct+c2 ·最小二乘法采取目标函数E(c,c,)=∑s,-ct,-c2=min 它隐含了在测量中,t是精确测量的,只有s,才测得不准确, 而在实际测量中,s都无法准确测量 。法向回归 -点(t,s)到直线s=ct+c,的距离为 iteh-6t-6 -c4-c2 /1+c (,s) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 8 法向回归 再看实验数据处理 一组测量数据(ti ,si ),欲拟和直线 • 最小二乘法采取目标函数 – 它隐含了在测量中,ti 是精确测量的,只有si 才测得不准确, 而在实际测量中ti ,si 都无法准确测量 • 法向回归 – 1 2 s ct c = + ( ) 2 n 1 2 i 1i 2 i 1 E c ,c s c t c min = = −−= ∑ 1 2 2 1 1 1 i i s ct c c − − + t s θ 1 2 s ct c = + (t s i i , ) i 1i 2 2 1 1 s ct c 1 c − − +
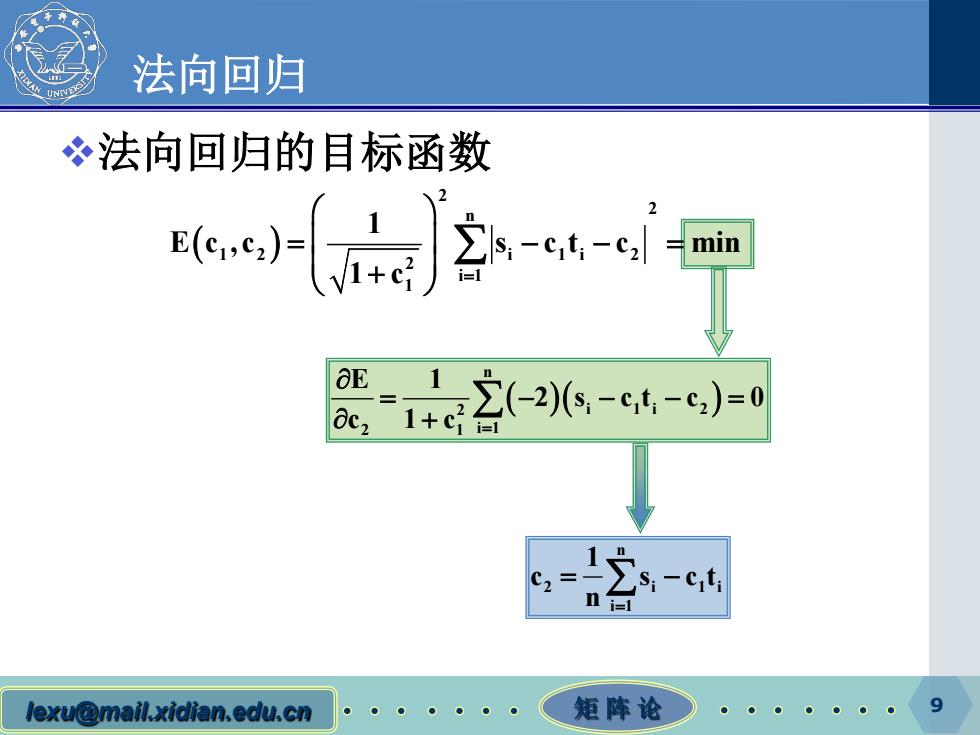
法向回归 冬法向回归的目标函数 o小空-t- =min (-2(,-ct-c)=0 i=1 lexu@mail.xidian.edu.cn ● 矩阵论 9
lexu@mail.xidian.edu.cn 矩 阵 论 9 法向回归 法向回归的目标函数 ( ) 2 2 n 1 2 i 1i 2 2 i 1 1 1 E c ,c s c t c min 1 c = = −−= + ∑ ( )( ) n 2 i 1i 2 2 1 i 1 E 1 2 s ct c 0 c 1c = ∂ = − −−= ∂ + ∑ n 2 i 1i i 1 1 c s ct n = = − ∑

法向回归 08e--+72--u a2-wuik-6-小 48--小-空--)客--》 a626--e+空-4-》 lexu@mail.xidian.edu.cn 矩阵论 。。。。。10
lexu@mail.xidian.edu.cn 矩 阵 论 10 法向回归 ( ) ( ) ( )( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) n n 2 1 2 i 1i 2 2 i i 1i 2 2 1 1 i 1 i 1 1 n 2 12 1i i i 1i 2 2 i 1 1 nnn 2 1 i 1i 2 1 i i 1i 2 i i 1i 2 2 i 1 i 1 i 1 1 n n 2 1 i i 1i 2 i i 2 i 1 i 1 1 E 2c 2 s ct c t s ct c c 1 c 1 c 2 cc cs t s ct c 1 c 2 cc s ct c c s s ct c t s ct c 1 c 2 c s s ct c t s 1 c = = = = = = = = ∂ = −− + − −− ∂ + + = −− −− + = − −− − −− − − + − = − −+ + ∑ ∑ ∑ ∑∑∑ ∑ ∑ - ( ct c 1i 2 ) 0 − − =