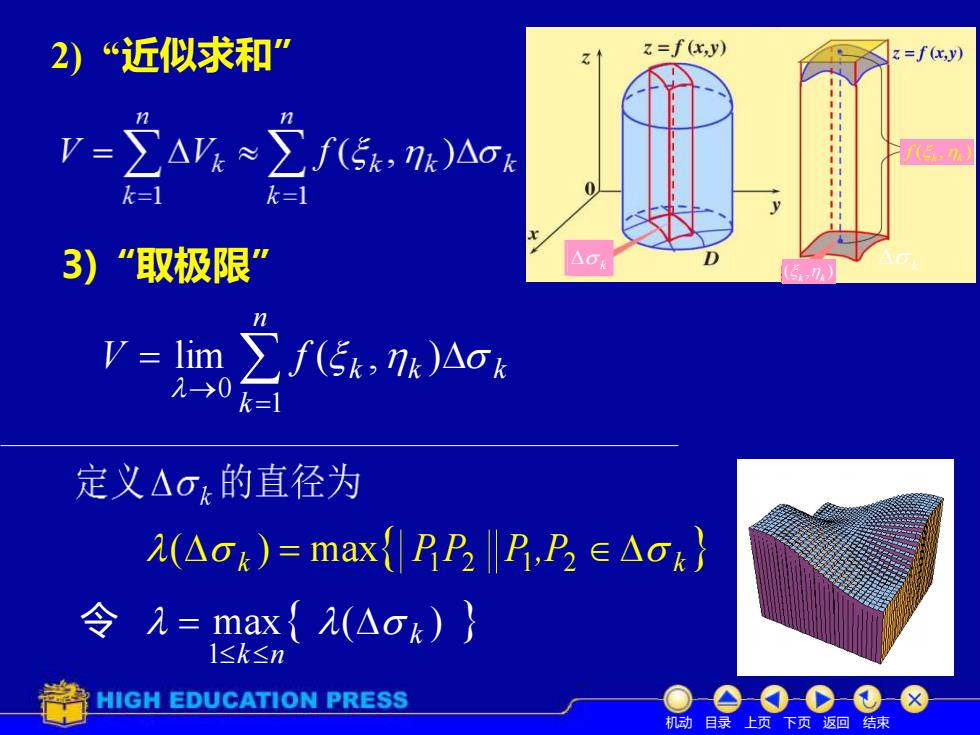
2)“近似求和” z=f(x,y) z=f(x,y) V=∑A≈∑5,)△a ,7 y 3)“取极限” △0 V=lim】 f5,)△o 2-→0 k=1 定义△o,的直径为 2(△ok)=max{☑DD,D∈△ok} 令2=max{(△ok)} 1≤k≤n HIGH EDUCATION PRESS 机动目录上页下页返回结束
3)“取极限” ( k ) = max P1P2 P1 ,P2 k 令 max ( ) 1 k k n = = → = n k k k k V f 1 0 lim ( , ) 机动 目录 上页 下页 返回 结束 2) “近似求和” k ( , ) k k k ( , ) k k f

2.平面薄片的质量 有一个平面薄片,在xoy平面上占有区域D,其面密 度为4(x,y)∈C,计算该薄片的质量M. 分析若4(x,y)≡4(常数),设D的面积为o,则M=4o 若4(x,y)≠常数,仍可用 “分割,近似求和,取极限”解决 1)“分割” 用任意曲线网分D为n个小区域Aoi,Ao2,·,△on, 相应把薄片也分为小区域 等HIGH EDUCATION PRESS 机动目 录上页下页返回结束
2. 平面薄片的质量 有一个平面薄片, 在 xoy 平面上占有区域 D , 度为 计算该薄片的质量 M . 设D 的面积为 , 则 M = 若 仍可用 其面密 “分割, 近似求和, 取极限”解决. 1) “分割” 用任意曲线网分D 为 n 个小区域 , , , , 1 2 n 相应把薄片也分为小区域 . D 机动 目录 上页 下页 返回 结束 y x 分析: 常数

2)“近似求和” 在每个△o中任取一点(5k,7k), △Mk≈u(5,刀k)△ok(k=1,2,.,n) 7=A含r5,noi 4)“取极限” M=lim ∑4(5k,7)Ao 入→>0 k=1 (5k,Ik)△OX 其中2=max{2(△ok)} lsk≤n HIGH EDUCATION PRESS 00C08 机动目录上页下页返回结束
2) “近似求和” 在每个 k 中任取一点 ( , ), k k = n k k k k 1 ( , ) 4) “取极限” → = = n k M k k k 1 0 lim ( , ) k ( , ) k k 机动 目录 上页 下页 返回 结束 max ( ) 1 k k n = 其中令 y x
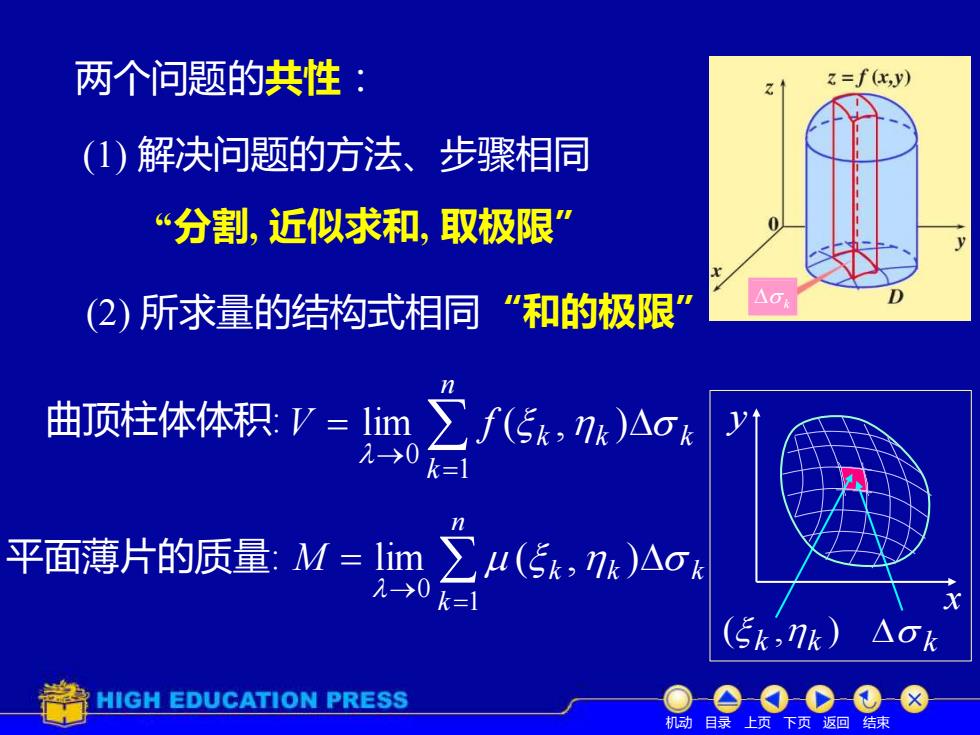
两个问题的共性: z=f(x,y) (1)解决问题的方法、步骤相同 “分割,近似求和,取极限 (2)所求量的结构式相同“和的极限” △ 曲顶柱体体积V=m∑f5,:)△c λ→0 k=1 平面薄片的质量M=lim∑4(5k,k)Ao 20k= (5k,7k) △Ok HIGH EDUCATION PRESS 机动目录上页下页返回结束
两个问题的共性: (1) 解决问题的方法、步骤相同 (2) 所求量的结构式相同 “分割, 近似求和, 取极限” = → = n k k k k V f 1 0 lim ( , ) → = = n k M k k k 1 0 lim ( , ) 曲顶柱体体积: 平面薄片的质量: 机动 目录 上页 下页 返回 结束 “和的极限” k k ( , ) k k y x