
第二节 第十二章 常款项级赵的审敘法 正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、交错级数及其审敛法 三、绝对收敛与条件收敛 第二节 一、正项级数及其审敛法 常数项级数的审敛法 机动 目录 上页 下页 返回 结束 第十二章

一、正项级数及其审敛法 0 如果级数 wm=a1+42++n+ 满足条件: n=1 4n≥0(n=1,2,.),称为正项级数。 S1=41≥0,S2=u1+u2≥41=S1, S3=u1+u2+u3≥u1+u2=S2 0≤S1≤S2≤S3≤.≤Sn-1≤S≤ 数列极限存在准则:单调有界数列必有极限 0 定理1.正项级数∑4n收敛,一部分和序列S, n= (n=1,2,.)有界 考HIGH EDUCATION PRESS
如果级数 n =1 un= u1 + u2 + + un + 满足条件: u 0 ( n = 1, 2 , ) , n 称为正项级数。 0 , s 1 = u1 2 u1 u2 s = + u1 3 u1 u2 u3 s = + + u1 + u2 , 1 = s 2 = s 0 s 1 s 2 s 3 s n−1 s n 一、正项级数及其审敛法 数列极限存在准则:单调有界数列必有极限 定理 1. 正项级数 收敛 部分和序列 有界
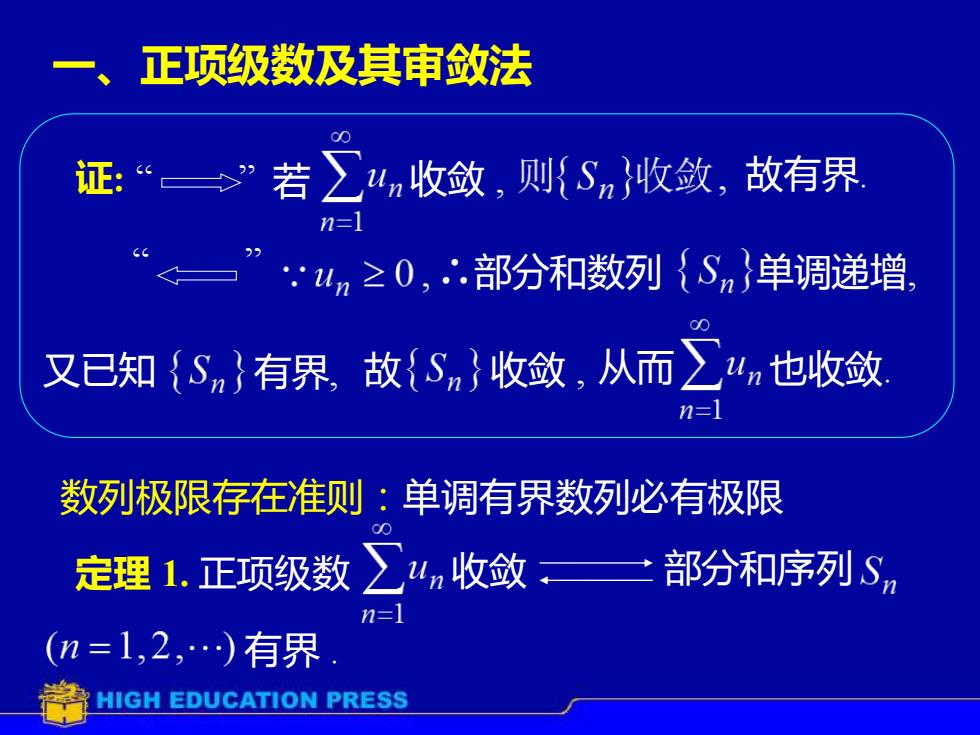
一、正项级数及其审敛法 证:“”若∑4n收敛,则{Sn}收敛,故有界 n=l n≥0,∴部分和数列{Sn}单调递增 又已知{Sn}有界故{Sn}收敛,从而∑4n也收敛 n=l 数列极限存在准则:单调有界数列必有极限 定理1.正项级数 ∑4n收敛 二部分和序列S n= (n=1,2,.)有界 学HIGH EDUCATION PRESS
一、正项级数及其审敛法 数列极限存在准则:单调有界数列必有极限 定理 1. 正项级数 收敛 部分和序列 有界 . 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 单调递增, 收敛 , 也收敛. 证: “ ” “
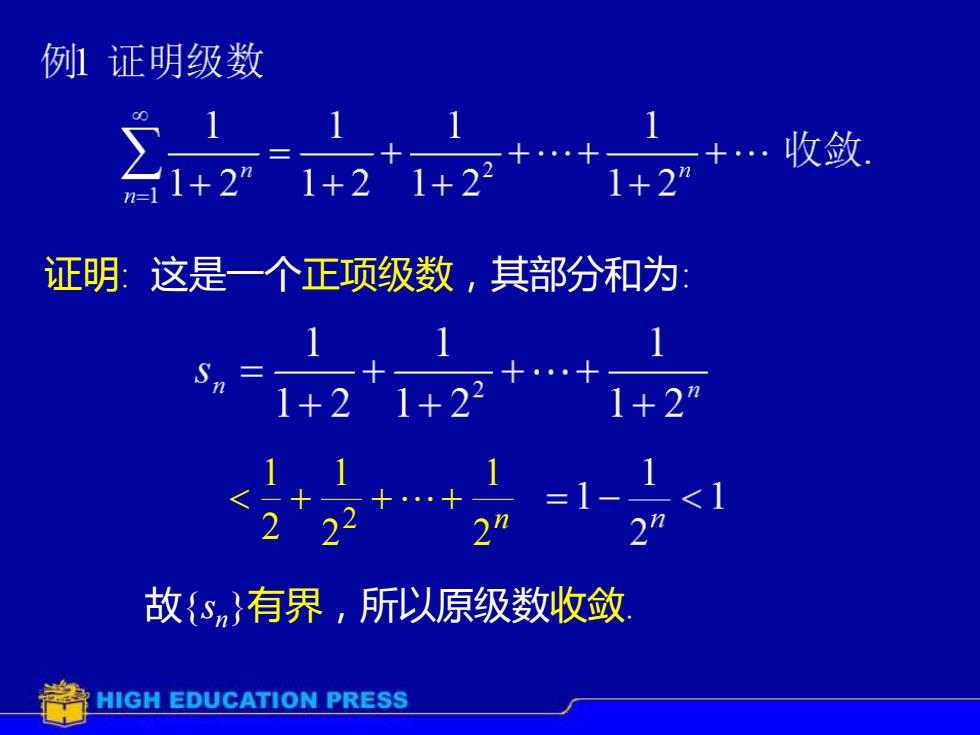
例列证明级数 证明:这是一个正项级数,其部分和为 Sn= 1+2 1+22 1+2” 故{s}有界,所以原级数收敛 HIGH EDUCATION PRESS
证明: 这是一个正项级数,其部分和为: 故{sn}有界,所以原级数收敛. n 2 1 2 1 2 1 2 + ++

定理2比较审敛法) 设∑un和∑yn都是正项级数, n= n=1 且un≤yn(n=1,2) (1)级数Σyn收敛,则级数 立n收敛: n=1 n=1 00 (2)级数∑4n发散,则级数∑yn发散 n=l n=1 即:大的收敛,小的一定收敛;小的发散,大的一定发散 推论:如果正项级数 ∑u和》Yn从某项N之后满 n=1 n=l 足关系式:u,≤ky,(k>0,n≥N)则定理2中的结论仍 成立。 HIGH EDUCATION PRESS
定理2 (比较审敛法) 设 和 都是正项级数, 且 u v (n = 1,2, ) n n n=1 n v n=1 n u (1) 级数 收敛,则级数 收敛; (2) 级数 发散,则级数 发散. n=1 n v n=1 n u n=1 n u n=1 n v 即: 大的收敛, 小的一定收敛; 小的发散, 大的一定发散. 推论: 如果正项级数 1 n n u = 1 n n v = ( 0, ) n n u k v k n N ,则定理2中的结论仍 和 从某项N之后满 足关系式: 成立