第十二章 无穷级数 数项级数 无穷级数 幂级数 傅里叶级数 表示函数 无穷级数是研究函数的工具 研究函数性质 数值计算
无穷级数 无穷级数 无穷级数是研究函数的工具 表示函数 研究函数性质 数值计算 数项级数 幂级数 傅里叶级数 第十二章

第一节 第十二章 常数项级数的橇念和性质 一、 常数项级数的概念 二、无穷级数的基本性质 三、级数收敛的必要条件 *四、柯西审敛原理 HIGH EDUCATION PRESS 是上页下页返回结束
常数项级数的概念和性质 一、常数项级数的概念 二、无穷级数的基本性质 三、级数收敛的必要条件 *四、柯西审敛原理 机动 目录 上页 下页 返回 结束 第一节 第十二章

一、常数项级数的概念 引例1.用圆内接正多边形面积逼近圆面积! 正六边形的面积C 正十二边形的面积:a1+a2 3×2”边形面积为 41+a2.+am n→o∞时,圆的面积A为: A=4+a2.+an+ 13、 3 3 310 100 1000 10 HIGH EDUCATION PRESS
一、常数项级数的概念 a1 + a2 1 3 3 3 3 3 10 100 1000 . 0 2 1 n = + + + + + a1 + a2 + an 引例1. 用圆内接正多边形面积逼近圆面积. 圆的面积 A 为: 正六边形的面积: 正十二边形的面积: A = a1 + a2 + an +

定义:给定一个数列4,42,.,4n,.将各项依 0 次相加,简记为 ∑4n,即 一般项 n=] 00 ∑4n=功1+42+++4n+. n=1 称上式为(常数项)无穷级数 级数的部分和 Sn=∑4k=功+2+3++4n级数的前n项和 k=1 部分和数列 S1=u1,S2=41+儿2,S3=41+42+儿3,., Sn=4+u2+.+um>. HIGH EDUCATION PRESS 机动目 上页下页返回结束
定义:给定一个数列 u1 , u2 , u3 , , un , 将各项依 , 1 n= n u 即 称上式为(常数项)无穷级数. 级数的前 n 项和 级数的部分和: 次相加, 简记为 机动 目录 上页 下页 返回 结束 一般项 部分和数列: , 1 u1 s = , 2 u1 u2 s = + , , s3 = u1 + u2 + u3 sn = u1 + u2 ++ un ,
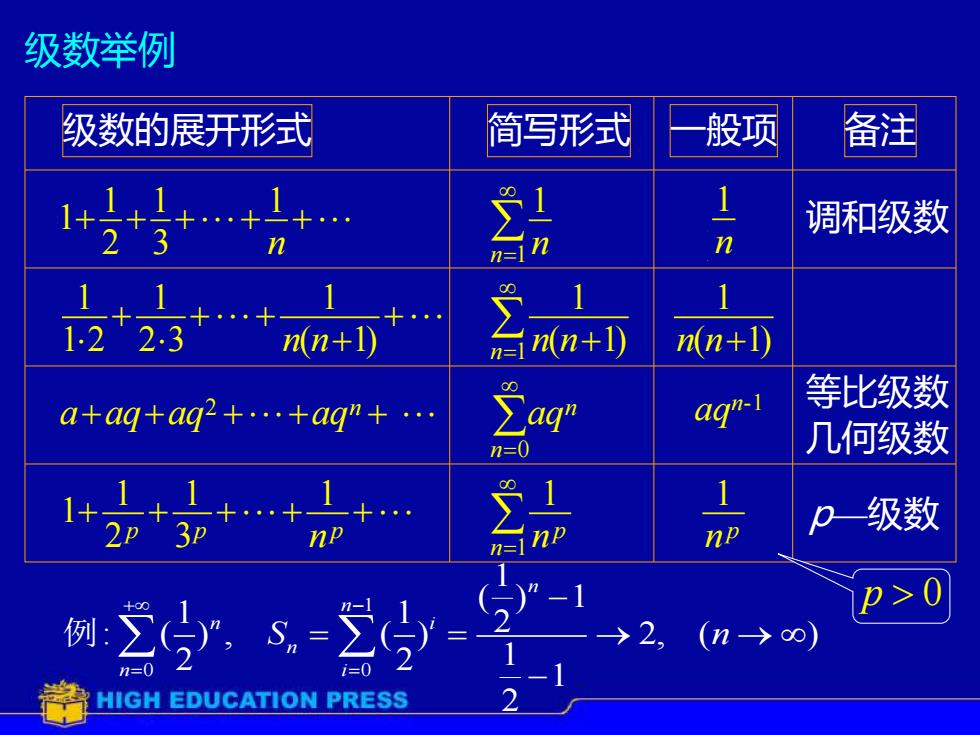
级数举例 级数的展开形式 简写形式 般项 备注 调和级数 n 11 12*23*.++ t. 含 n(n+1) a+ag+ag2+.+aq"+. ag"-I 等比级数 n=0 几何级数 1+动 铝 np p一级数 例 三s- ()”-1 p>0 →2, () HIGH EDUCATION PRESS
级数举例 1 3 1 2 1 1 1 1 = + + + + + n= n n 1 3 1 2 1 1 1 1 = + + + + + n= n n 1 3 1 2 1 1 1 1 = + + + + + n= n n 调和级数 ( 1) 1 2 3 1 1 2 1 ( 1) 1 1 + + + + + + ( 1) n= n n n n 1 2 3 1 1 2 1 ( 1) 1 1 + + + + + + n= n n n n ( 1) 1 2 3 1 1 2 1 ( 1) 1 1 + + + + + + n= n n n n 2 0 = + + + + + = n n n aq a aq aq aq 2 0 = + + + + + = n n n aq a aq aq aq 几何级数 1 3 1 2 1 1 1 1 + + + + + = p p p n np n 1 3 1 2 1 1 1 1 + + + + + = p p p n np n 1 3 1 2 1 1 1 1 + + + + + = p p p n np n 级数的展开形式 简写形式 一般项 备注 aqn-1 等比级数 p—级数 1 0 0 1 ( ) 1 1 1 2 : ( ) , ( ) 2, ( ) 2 2 1 1 2 n n n i n n i S n + − = = − = = → → − 例 p 0