
01数列极限的定义COAORA人邮教育定义1.6(描述性定义)对于数列(x当n无限增大(n??)时,若x无限趋近于一个确定的常数a,则称α为数列(x的极限(或称数列收敛于α),记作limx,=a或x,?a(n??)nR此时,也称数列(x的极限存在;否则,称数列{x,}的极限不存在(或称数列是发散的)
6 对于数列 , 当 无限增大 时,若 无限 (或称数列收敛于 ), 极限不存在(或称数列是发散的). . 趋近于一个确定的常数 ,则称 为数列 的极限 记作 此时,也称数列 的极限存在;否则,称数列 的 定义1. 6(描述性定义) 01 数列极限的定义

01OOOOR数列极限的定义人邮教育例下面各数列,哪些数列收敛,哪些数列发散?对于收敛数列,通过观察通项的变化趋势,写出它们的极限n(1)x.n+1收敛n+(- 1)"- I(2).X,n(3)X,=2"发散X, = (- 1)"-1(4)
7 01 数列极限的定义 收敛 发散 (1) (2) (4) 下面各数列,哪些数列收敛,哪些数列发散? 对于收敛数列,通过观察通项的变化趋势,写 出它们的极限. 例 1 (3)

01COAO数列极限的定义RA人邮教育定义1.6(描述性定义)当n无限增大(n??)时,若x,无限对于数列(x,)趋近于一个确定的常数a则称α为数列x,的极限(或称数列收敛于α),记作limx,=a或x,?a(n?)nRY
9 对于数列 , 当 无限增大 时,若 无限 (或称数列收敛于 ), . 趋近于一个确定的常数 ,则称 为数列 的极限 记作 定义1. 6(描述性定义) 01 数列极限的定义
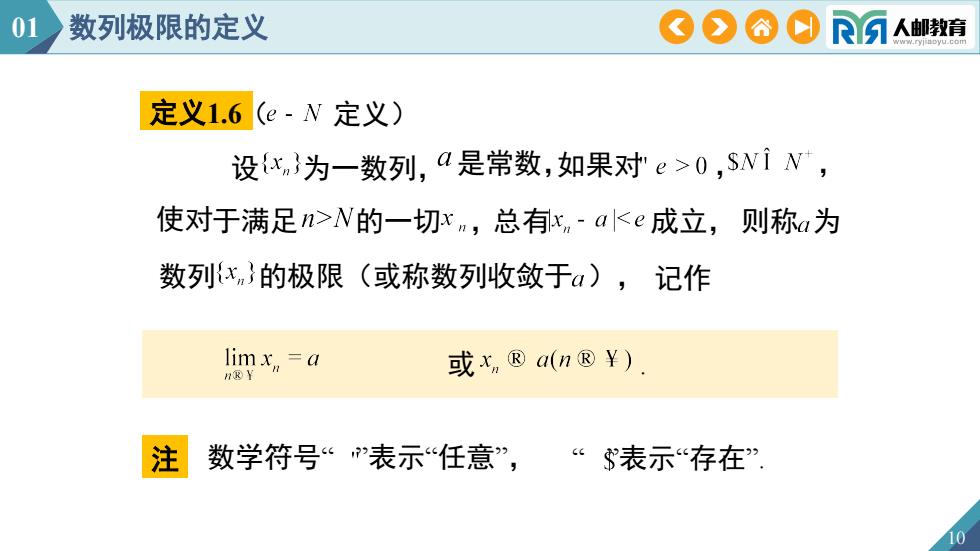
01数列极限的定义COAOR人邮教育定义1.6(e-N定义)设(x,}为一数列,α是常数,如果对"e>0,siN使对于满足n>N的一切xn,总有x,-a<e成立,则称a为数列(x,)的极限(或称数列收敛于α),记作limx,=a或x,a(n??)nRY注数学符号“"表示“任意”,“$表示“存在
或 . 10 数列 的极限(或称数列收敛于 ), 定义1.6( 定义) 注 设 为一数列, 是常数,如果对 , , 数学符号“ ”表示“任意” , “ ”表示“存在”. 记作 01 数列极限的定义 使对于满足 的一切 ,总有 成立, 则称 为
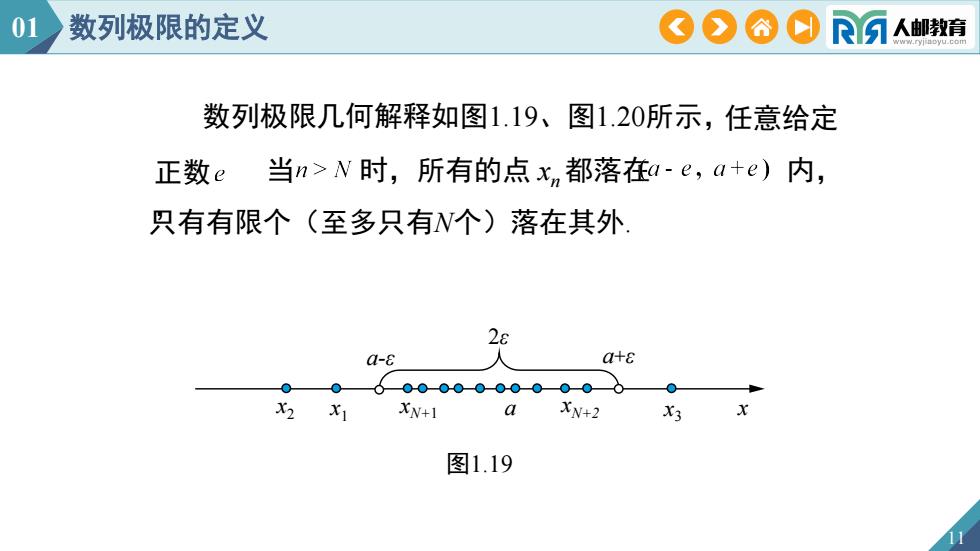
01数列极限的定义COOO人邮教育数列极限几何解释如图1.19、图1.20所示,任意给定当n>N时,所有的点x,都落在a-e,a+e)内,正数e只有有限个(至多只有N个)落在其外26人a+ea-c·XN+2X2XN+1axXiX3图1.19
2ε a-ε 11 数列极限几何解释如图1.19、图1.20所示, 只有有限个(至多只有N个)落在其外. x2 xN+1 a x a+ε x3 x x1 N+2 任意给定 当 时,所有的点 x 正数 n 都落在 内, , 图1.19 01 数列极限的定义