
高等数学(上册)第2章导数与微分第4节函数的微分人民邮电出版社POSTS&TELECOMPRESS
高等数学(上册) 第4节 函数的微分 第2章 导数与微分

R人邮教育本讲内容w.ryjinoyu.c01微分的概念02微分的几何意义03微分的计算04微分的应用
01 微分的概念 02 微分的几何意义 03 微分的计算 04 微分的应用 本 讲 内 容

一、微分的概念引例:一块正方形金属薄片受温度变化的影响,其边长由xo变到xo口□x,问此薄片面积改变了多少?设薄片边长为x,面积为A,则Ax2,当x在xo取得增量x时,面积的增量为XoxXA (x。x)?x22xox (x)LxXoAxoXox口0时为关于△x 的高阶无穷小线性函数故A2xx称为函数在Xo的微分HIGH EDUCATION PRESS
一、微分的概念 引例: 一块正方形金属薄片受温度变化的影响, 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 面积的增量为 关于△x 的 线性函数 高阶无穷小 时为 故 称为函数在 的微分 当 x 在 取 得增量 时, 边长由 变到 其

01微分的概念OOOORA人邮教育定义2.4设函数=f(x)在xo的某邻域U(xo)内有定义,x+DxiU(xo),若函数增量Dy=f(x。+Dx)-f(xo)可表示为(2. 4)Dy = ADx + o(Dx)其中A是不依赖于Dx的常数,而o(Dx)是比Dx高阶的无穷小,那么称函数y=f(x)在点xo是可微的.而ADx叫做函数f(x)在点xo相应于自变量增量Dx的微分,记作dylx=xo或df(x)x=xo"即dy =xo =ADx
定义2. 4 4 设函数 在 的某邻域 内有定义, , 若函数增量 可表示为 (2. 4) 其中 A 是不依赖于 的常数,而 那么称函数 在点 是可微的. 是比 高阶的无穷小, 而 叫做函数 在 01 微分的概念 点 相应于自变量增量 的微分,记作 dy|x=x0 或 d f (x)| x=x0, 即
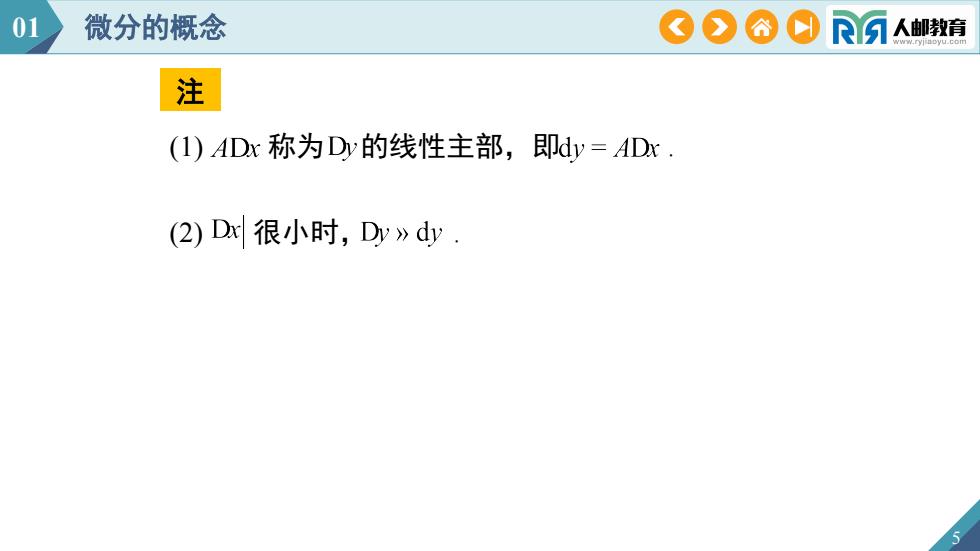
01微分的概念COARA人邮教育注(1)ADx称为Dy的线性主部,即dy=ADx(2) Dx很小时,Dy》dy
注 5 (2) 很小时, . 01 微分的概念 (1) 称为 的线性主部,即