
2、奇偶性 VxeD,且有-x∈D, 若∫(-x)=∫(x),则称f(x)为偶函数 若f(-x)=-f(x),则称f(x)为奇函数 说明:若f(x)在x=0有定义, 则当f(x)为奇函数时, 必有f(0)=0
xD, 且有 − xD, 若 则称 f (x) 为偶函数; 若 则称 f (x) 为奇函数. 说明: 若 f (x) 在 x = 0 有定义 , f (0) = 0. f (x) 为奇函数时, x y 则当 − x O x 必有 2、奇偶性
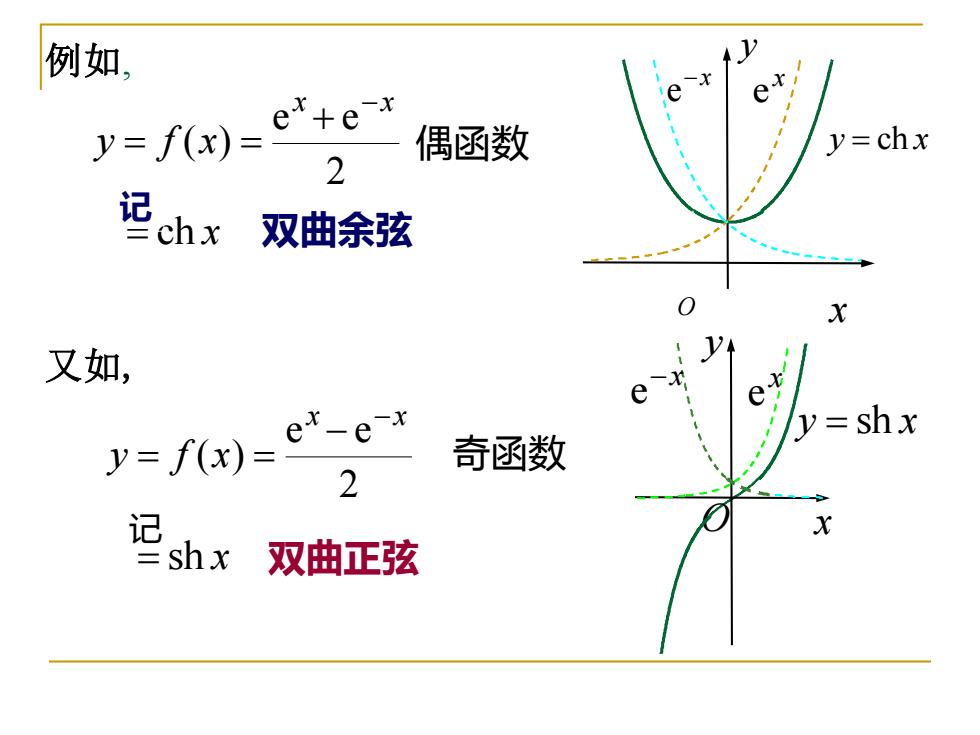
例如, y=f(x)= ex+e-x 偶函数 y=chx 2 chx 双曲余弦 X 又如, y=shx y=f(x)= ex-e-x 奇函数 2 记 X shx 双曲正弦
例如, 2 e e ( ) x x y f x − + = = = ch x 偶函数 x y O x e −x e y = ch x 双曲余弦 记 又如, 奇函数 = sh x 双曲正弦 记 x y O x e −x e y = sh x 2 e e ( ) x x y f x − − = =