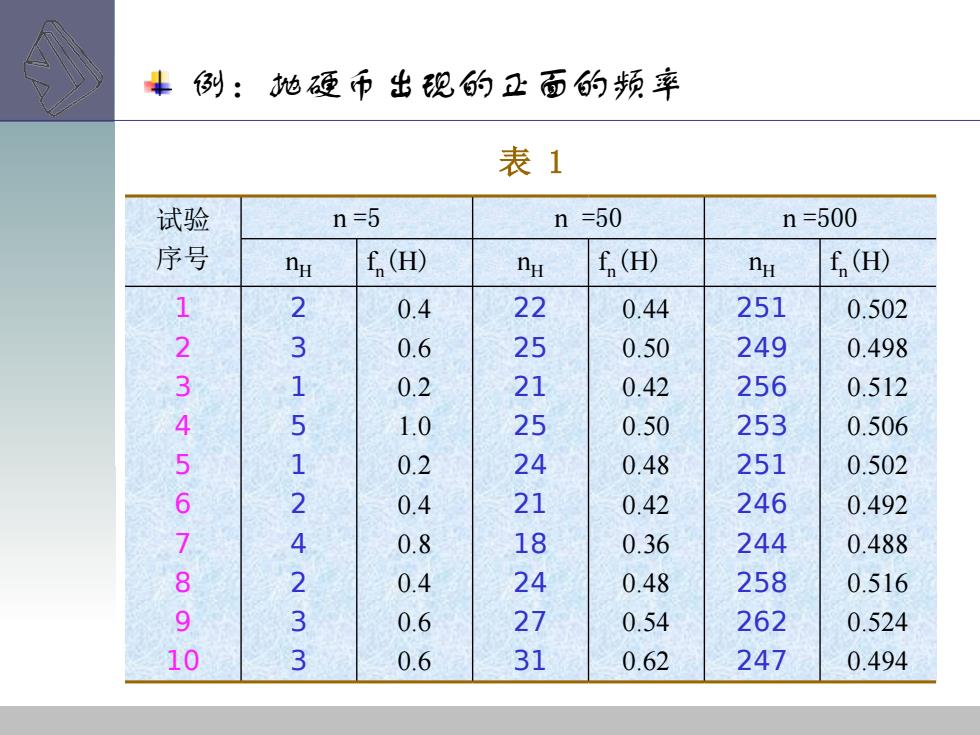
集例:抛地硬币出现的正面的频率 表1 试验 n=5 n=50 n=500 序号 DH £(HD) DH f (H) na (H) 2 0.4 22 0.44 251 0.502 123456 3 0.6 25 0.50 249 0.498 1 0.2 0.42 256 0.512 5 1.0 25 0.50 253 0.506 1 0.2 24 0.48 251 0.502 2 0.4 21 0.42 246 0.492 7890 4 0.8 18 0.36 244 0.488 2 0.4 0.6 21 0.48 258 0.516 0.54 262 0.524 3 0.6 31 0.62 247 0.494
试验 序号 n =5 n =50 n =500 nH f n(H) nH f n(H) nH f n(H) 1 2 3 4 5 6 7 8 9 10 2 3 1 5 1 2 4 2 3 3 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.4 0.6 0.6 22 25 21 25 24 21 18 24 27 31 0.44 0.50 0.42 0.50 0.48 0.42 0.36 0.48 0.54 0.62 251 249 256 253 251 246 244 258 262 247 0.502 0.498 0.512 0.506 0.502 0.492 0.488 0.516 0.524 0.494 表 1 例:抛硬币出现的正面的频率
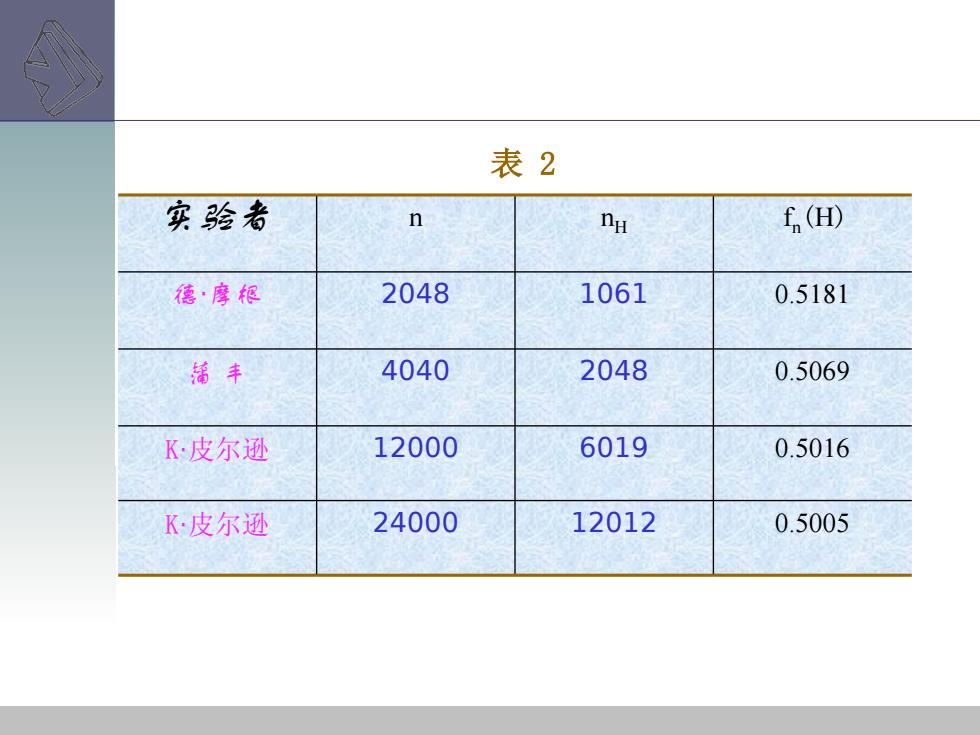
表2 实验者 n n f (H) 德·摩根 2048 1061 0.5181 福丰 4040 2048 0.5069 K·皮尔逊 12000 6019 0.5016 K皮尔逊 24000 12012 0.5005
实验者 n nH f n(H) 德·摩根 2048 1061 0.5181 蒲 丰 4040 2048 0.5069 K·皮尔逊 12000 6019 0.5016 K·皮尔逊 24000 12012 0.5005 表 2

**频率的性质: 10£f(A)£1 2f(S)=1 3若A,A,A,两两互不相容,则n(UA)=8fn(A) i= 且f,()随n的增大渐趋稳定,记稳定值为p
** 频率的性质: 且 随n的增大渐趋稳定,记稳定值为p.

概率 设E是随机试验,S是它的样本空间.对于E 的每一事件A赋予一个实数,记为P(),称为事 件A的概率,如果集合函数P(为满足下列条件 1P0£P(A)非负性) 2”P(S)=(规范性) 3若可列个事件A,A,L,AL两两互不相容 则P(UA,)=aP(AX可列可加性) 则称P(A)是事件A发生的概率
(二) 概率 则称P(A)是事件A发生的概率

(三)概率的基本性质 (1)P(F)0 证明:取可列个事件A,A,KAK,令所有的A=F, +¥ 则AA,=F,即A,AKAK是不相容事件组且UA=F, k-=1 由概率的非负性,有P(F)30,再由概率的可列可加性得: +¥ P(U=F)P(4)=P(F). k-1 k=1 k-1 要使得上式成立当且仅当P(F)=0.得证
(三)概率的基本性质