
导 4.共线向量与共面向量 (1)两个向量共线(平行)的充要条件:对任意两个空间向量 a,b(b0),allb的充要条件是存在实数,使 (2)直线的方向向量:如图,O是直线1上一点,在直线1上取非零 向量a,则对于直线l上任意一点P,存在实数2,使得0P= 我们把与向量a平行的非零向量称为直线的
导航 4.共线向量与共面向量 (1)两个向量共线(平行)的充要条件:对任意两个空间向量 a,b(b≠0),a∥b的充要条件是存在实数λ,使 a=λb . (2)直线的方向向量:如图,O是直线l上一点,在直线l上取非零 向量a,则对于直线l上任意一点P,存在实数λ,使得 = λa . 我们把与向量a平行的非零向量称为直线l的 方向向量 . 𝑂 𝑃
导航 3)与直线、平面平行的向量:如图,如果表示向量a的有向线 段OA所在的直线OA与直线1 或 ,那么称向 量a平行于直线l.如果直线OA 或 ,那么称向量a平行于平面u A a
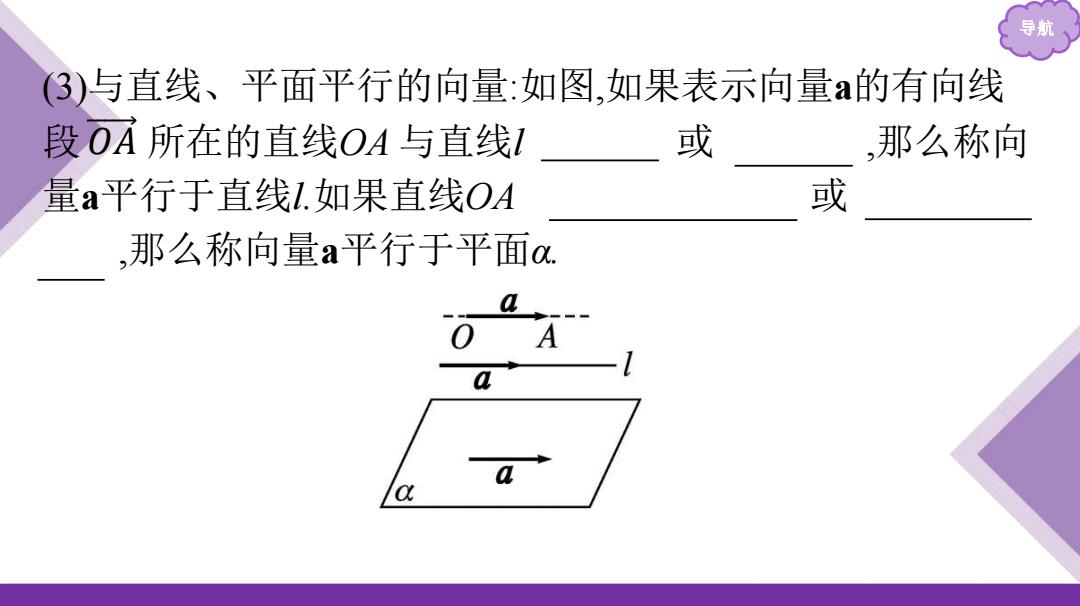
导航 (3)与直线、平面平行的向量:如图,如果表示向量a的有向线 段 所在的直线OA 与直线l 平行 或 重合 ,那么称向 量a平行于直线l.如果直线OA 平行于平面α 或 在平面α 内 ,那么称向量a平行于平面α. 𝑂 𝐴

导航 4)共面向量:平行于 的向量,叫做共面向量。 (5)三个向量共面的充要条件:如果两个向量a,b ,那 么向量p与向量a,b共面的充要条件是存在唯一的有序实数对 (x,y),使p=
导航 (4)共面向量:平行于 同一个平面 的向量,叫做共面向量. (5)三个向量共面的充要条件:如果两个向量a,b 不共线 ,那 么向量p与向量a,b共面的充要条件是存在唯一的有序实数对 (x,y),使p= xa+yb

导航 课堂·重难突破 空间向量的有关概念 典例剖析 1.下列说法正确的是( A.若a=b,则a,b的模相等,方向相同或相反 B.若向量a是向量b的相反向量,则a=b C.不相等的两个空间向量的模必不相等 D.在四边形ABCD中,一定有AB+AD=AC 答案:B
导航 课堂·重难突破 一 空间向量的有关概念 典例剖析 1.下列说法正确的是( ) A.若|a|=|b|,则a,b的模相等,方向相同或相反 B.若向量a是向量b的相反向量,则|a|=|b| C.不相等的两个空间向量的模必不相等 D.在四边形 ABCD 中,一定有𝐴 𝐵 + 𝐴 𝐷 = 𝐴 𝐶 答案:B

导航 解析:对于A,由a=b,可知a,b的模相等,但方向不确定,故A错 误;对于B,因为a=-b,所以a=b,故B正确;C显然错误;对于D, 只有当四边形ABCD为平行四边形时,才有AB+AD=AC,故 D错误.故选B
导航 解析:对于A,由|a|=|b|,可知a,b的模相等,但方向不确定,故A错 误;对于B,因为a=-b,所以|a|=|b|,故B正确;C显然错误;对于D, 只有当四边形ABCD为平行四边形时,才有 ,故 D错误.故选B. 𝐴 𝐵 + 𝐴 𝐷 = 𝐴 𝐶