
导航 微思考空间向量的定义及表示方法与平面向量的定义及表示 方法有区别吗? 提示:空间向量与平面向量的定义没有本质区别,表示方法都 一样
导航 微思考空间向量的定义及表示方法与平面向量的定义及表示 方法有区别吗? 提示:空间向量与平面向量的定义没有本质区别,表示方法都 一样
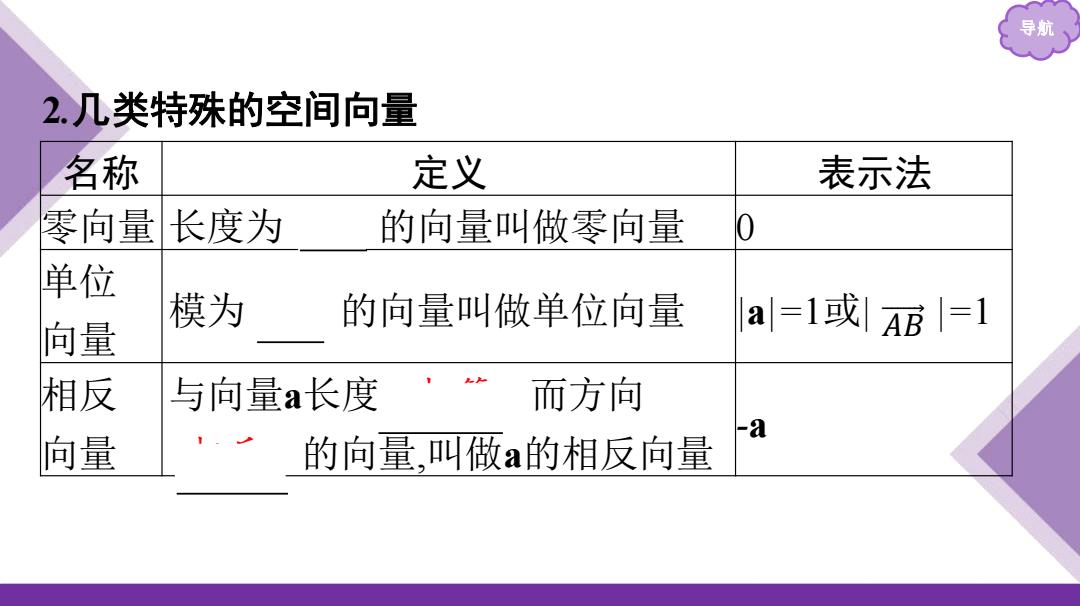
导航 2.几类特殊的空间向量 名称 定义 表示法 零向量长度为 的向量叫做零向量 0 单位 模为 的向量叫做单位向量 向量 a=1或|AB=1 相反 与向量a长度 而方向 -a 向量 的向量,叫做a的相反向量
导航 2.几类特殊的空间向量 名称 定义 表示法 零向量 长度为 0 的向量叫做零向量 0 单位 向量 模为 1 的向量叫做单位向量 |a|=1或| |=1 相反 向量 与向量a长度 相等 而方向 相反 的向量,叫做a的相反向量 -a 𝐴 𝐵

导航 名称 定义 表示法 如果表示若干空间向量的有向线段 共线 所在的直线互相平行或重合,那么这aIb 向量 些向量叫做共线向量或平行向量 规定:零向量与任意向量平行 011 a 相等 方向” 且模 的向量 向量 叫做相等向量 a=b或AB=CD
导航 名称 定义 表示法 共线 向量 如果表示若干空间向量的有向线段 所在的直线互相平行或重合,那么这 些向量叫做共线向量或平行向量 a∥b 规定:零向量与任意向量平行 0∥a 相等 向量 方向 相同 且模 相等 的向量 叫做相等向量 a=b或 𝐴 𝐵 = 𝐶 𝐷
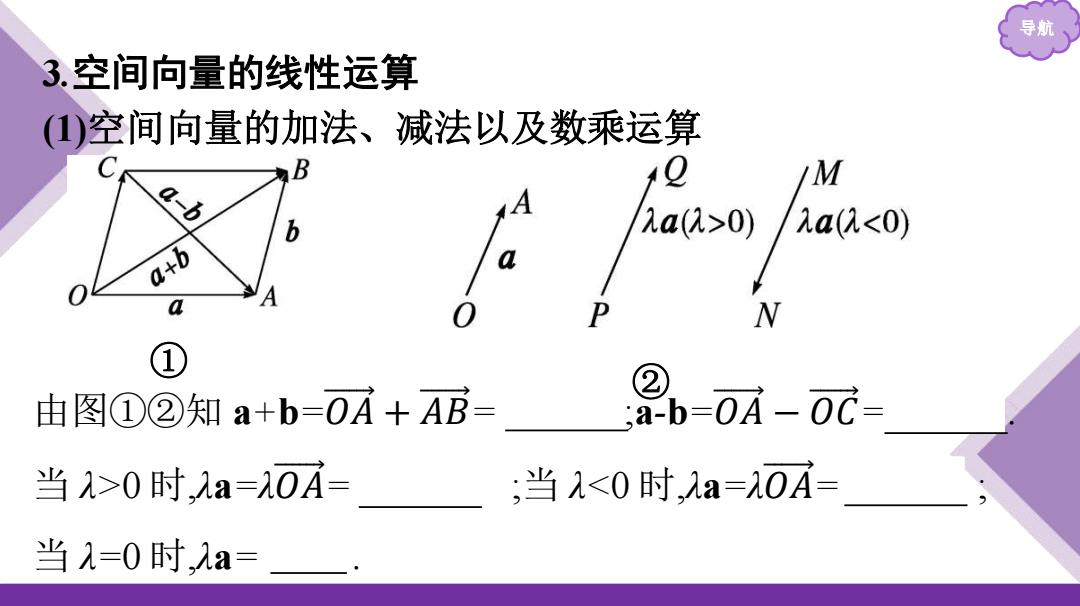
导航 3.空间向量的线性运算 ()空间向量的加法、减法以及数乘运算 M 2a(2>0) 1a(2<0) a+b N ① 由图①②知a+b=0A+AB= 2-0iA-0c- 当1>0时,1a=0A= ;当1<0时,λa=0A= 当λ=0时,λa=
导航 3.空间向量的线性运算 (1)空间向量的加法、减法以及数乘运算 ① ② 由图①②知 a+b=𝑂 𝐴 + 𝐴 𝐵 = 𝑂 𝐵 ;a-b=𝑂 𝐴 − 𝑂 𝐶 = 𝐶 𝐴 . 当 λ>0 时,λa=λ𝑂 𝐴 = 𝑃 𝑄 ;当 λ<0 时,λa=λ𝑂 𝐴 = 𝑀 𝑁 ; 当 λ=0 时,λa= 0

导航 (2)空间向量的线性运算满足以下运算律(其中2u∈R) 交换律:a+b=b+a, 结合律:a+(b+c)=(a+b)+c,(ua)=(u)a, 分配律:(+)a=a+ua,λ(a+b)=人a+2b. 微训练化简:5(3a-2b)+4(2b-3a)=
导航 (2)空间向量的线性运算满足以下运算律(其中λ,μ∈R): 交换律:a+b=b+a; 结合律:a+(b+c)=(a+b)+c,λ(μa)=(λμ)a; 分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb. 微训练化简:5(3a-2b)+4(2b-3a)= 3a-2b