
全程设计 第2课时 用空间向量研究夹角问题
第2课时 用空间向量研究夹角问题
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
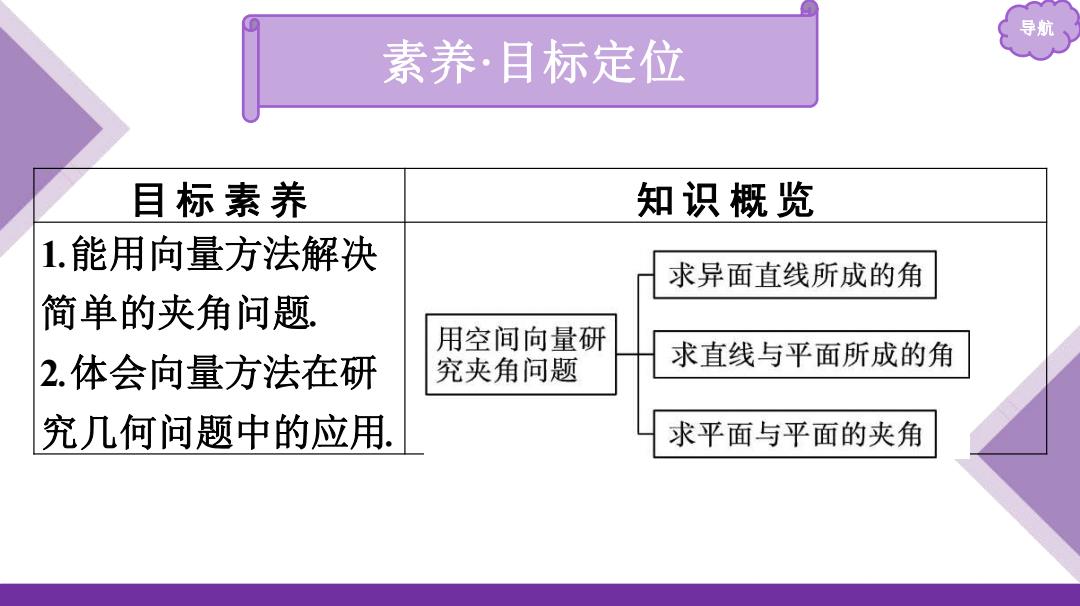
导航 素养·目标定位 目标素养 知识概览 1.能用向量方法解决 求异面直线所成的角 简单的夹角问题 用空间向量研 2.体会向量方法在研 究夹角问题 求直线与平面所成的角 究几何问题中的应用. 求平面与平面的夹角
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用向量方法解决 简单的夹角问题. 2.体会向量方法在研 究几何问题中的应用

导航 课前·基础认知 1.异面直线所成的角 若异面直线l1,1,所成的角为0,其方向向量分别是u,V,则 cos 0=cos<u,v>= luv u☑l 2.直线与平面所成的角 直线与平面相交,设直线与平面所成的角为0,直线的方向向量 为u,平面的法向量为n,则sin0=|cos<u,n>= lun lullnl
导航 课前·基础认知 1.异面直线所成的角 若异面直线l1 ,l2所成的角为θ,其方向向量分别是u,v,则 cos θ=|cos<u,v>|= . |𝑢·𝑣| |𝑢||𝑣| 2.直线与平面所成的角 直线与平面相交,设直线与平面所成的角为θ,直线的方向向量 为u,平面的法向量为n,则sin θ=|cos<u,n>|= . |𝑢·𝑛| |𝑢||𝑛|

导月 3.平面与平面的夹角 ()平面与平面的夹角的定义 平面α与平面B相交,形成四个二面角,我们把这四个二面角中 的二面角称为平面a与平面B的夹角 (2)平面与平面的夹角的求法 若平面a,B的法向量分别是n,和n2,则平面a与平面B的夹角即 为向量n,和n2的夹角或其补角.设平面a与平面的夹角为0,则 cos 0=cos<n,n2= ni'n2l Inillnzl
导航 3.平面与平面的夹角 (1)平面与平面的夹角的定义 平面α与平面β相交,形成四个二面角,我们把这四个二面角中 不大于90° 的二面角称为平面α与平面β的夹角. (2)平面与平面的夹角的求法 若平面α,β的法向量分别是n1和n2 ,则平面α与平面β的夹角即 为向量n1和n2的夹角或其补角.设平面α与平面β的夹角为θ,则 cos θ=|cos<n1 ,n2>|= . |𝑛1 ·𝑛2| |𝑛1||𝑛2|