
全程设计 第2课时 平面与平面垂直的性质定理
第2课时 平面与平面垂直的性质定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 平面与平面垂直的性质定理 文字 两个平面垂直,如果 有一直 语言 线垂直于这两个平面的 ,那么这条 直线与另一个平面
导航 课前·基础认知 平面与平面垂直的性质定理 文字 语言 两个平面垂直,如果 一个平面内 有一直 线垂直于这两个平面的 交线 ,那么这条 直线与另一个平面 垂直
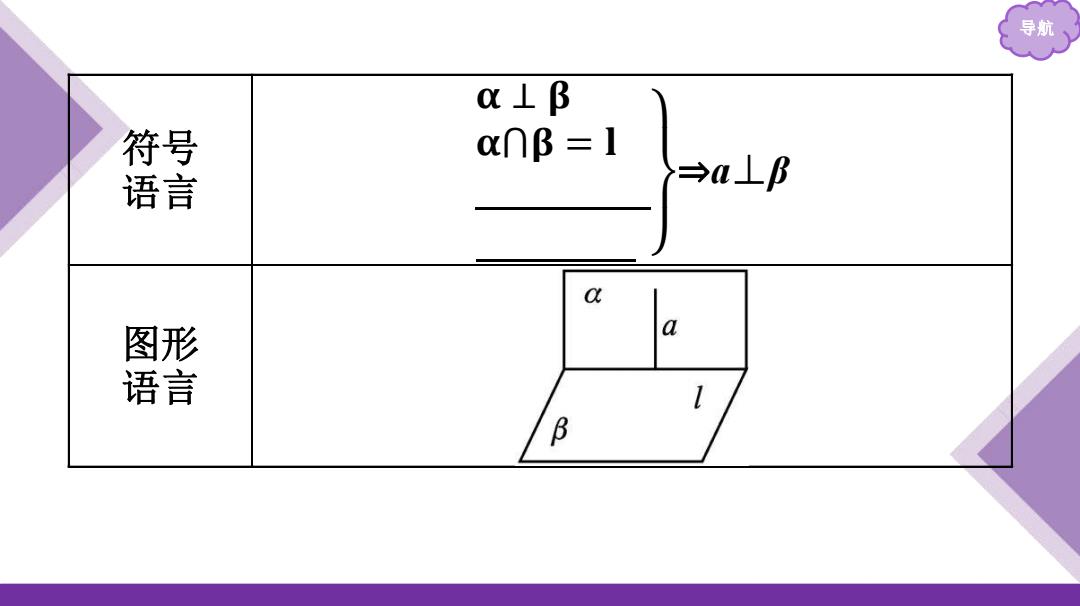
导航 o⊥β 冒 o∩B=1 →a⊥阝 a a 竖 β
导航 符号 语言 𝛂 ⊥ 𝛃 𝛂⋂𝛃 = 𝐥 𝐚 ⊂ 𝛂 𝐚 ⊥ 𝐥 ⇒a⊥β 图形 语言

导航 微思考若a⊥B,则a内的直线必垂直于内的无数条直线吗? 提示:正确.若设a∩B=l,aca,bcf,b⊥I,则a⊥b,故B内与b平行 的无数条直线均垂直于α内的任意直线 微拓展平面与平面垂直的性质定理揭示了面面垂直、线面 垂直及线线垂直间的内在联系,体现了数学中的化归、转化 思想,其转化关系如下: 线面垂直判定 面面垂直判定 线线垂直 线面垂直 面面垂直 线面垂直的 面面垂直的 定义是线线 性质是线面 垂直的判定 垂直的判定
导航 微思考 若α⊥β,则α内的直线必垂直于β内的无数条直线吗? 提示:正确.若设α∩β=l,a⊂α,b⊂β,b⊥l,则a⊥b,故β内与b平行 的无数条直线均垂直于α内的任意直线. 微拓展平面与平面垂直的性质定理揭示了面面垂直、线面 垂直及线线垂直间的内在联系,体现了数学中的化归、转化 思想,其转化关系如下: