
全程设计 第2课时】 用空间向量研究直线、平面 的垂直关系
第2课时 用空间向量研究直线、平面 的垂直关系
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 知识概览 1.能用向量语言表述直 线与直线、直线与平面、 平面与平面的垂直关系. 用空间向量证明线线垂直 2.会用直线的方向向量 用空间向量研 究直线、平面 用空间向量证明线面垂直 及平面的法向量证明直 的垂直关系 用空间向量证明面面垂直 线与直线、直线与平面 及平面与平面的垂直问 题
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用向量语言表述直 线与直线、直线与平面、 平面与平面的垂直关系. 2.会用直线的方向向量 及平面的法向量证明直 线与直线、直线与平面 及平面与平面的垂直问 题
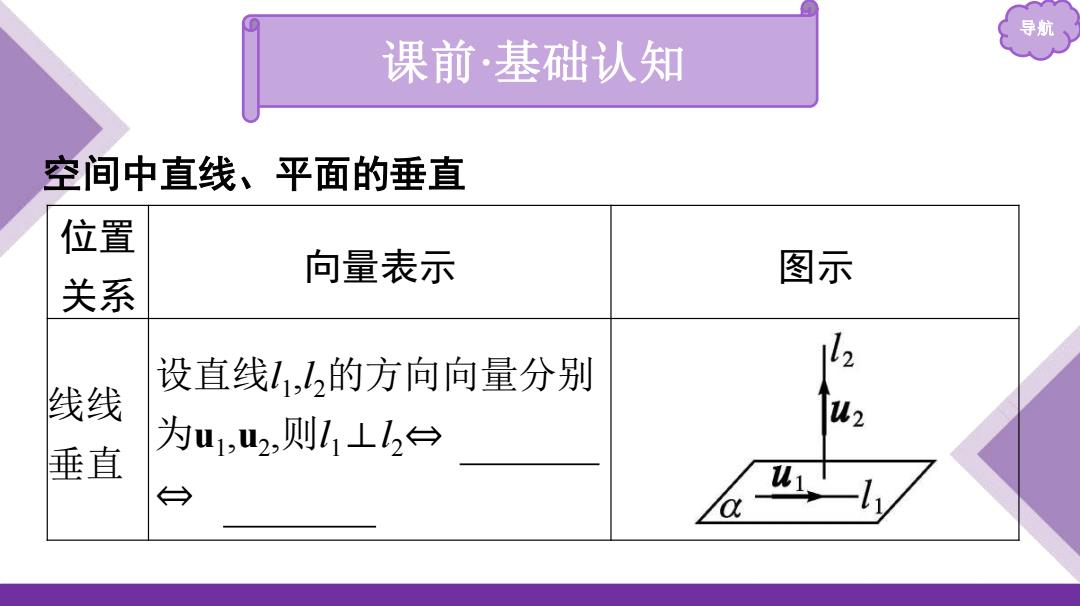
导航 课前·基础认知 空间中直线、平面的垂直 位置 向量表示 图示 关系 设直线1,1,的方向向量分别 12 线线 为u1,2,则l1⊥12→ u2 垂直 台
导航 课前·基础认知 空间中直线、平面的垂直 位置 关系 向量表示 图示 线线 垂直 设直线l1 ,l2的方向向量分别 为u1 ,u2 ,则l1⊥l2⇔ u1⊥u2 ⇔ u1·u2 =0
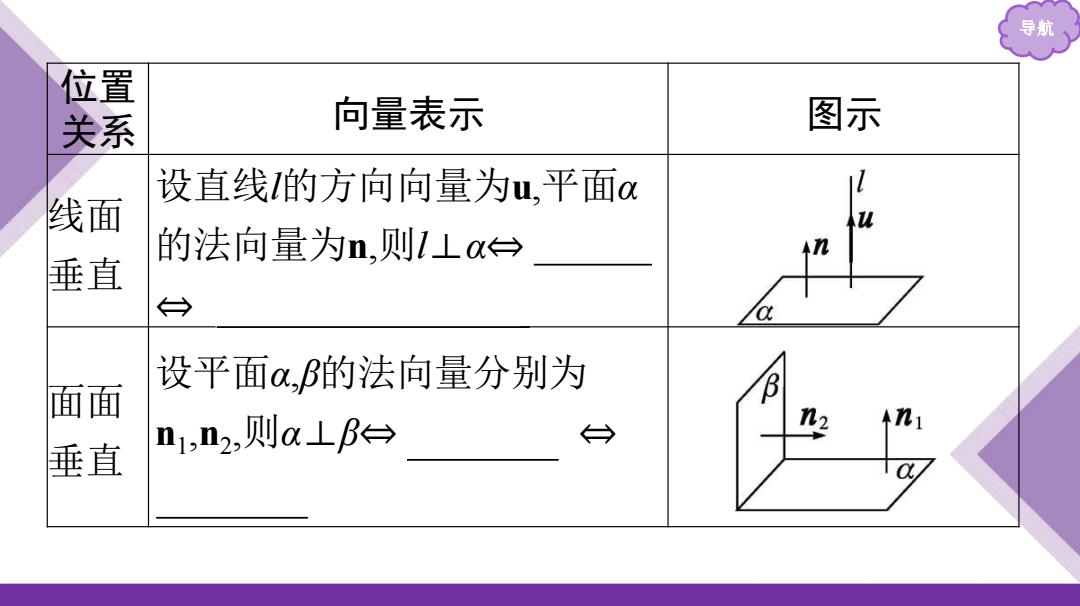
导航 位置 关系 向量表示 图示 设直线的方向向量为u,平面 线面 的法向量为n,则1La台 垂直 → 设平面α,B的法向量分别为 面面 B n1,n2,则a⊥B台 ←→ 2 垂直
导航 位置 关系 向量表示 图示 线面 垂直 设直线 l的方向向量为 u ,平面 α 的法向量为 n , 则 l ⊥ α ⇔ u ∥ n ⇔ ∃ λ ∈ R ,使得 u = λ n 面面 垂直 设平面 α ,β的法向量分别为 n 1 , n 2 , 则 α ⊥ β ⇔ n 1 ⊥ n 2 ⇔ n 1 · n 2 = 0