《线性代数》课程教学课件（讲稿，B）第四章 线性方程组 §4.2 齐次线性方程组

第四章线性方程组 §4.2齐次线性方程组 齐次线性方程组解的性质 二 、基础解系及其求法 三、小结

第四章 线性方程组 三、小结 二、基础解系及其求法 一、齐次线性方程组解的性质 §4.2 齐次线性方程组

第四章线性方程组 齐次线性方程组解的性质 设有齐次线性方程组 01X1+012X2+.+41nXn=0 21x1+22X2+.+2mXn=0 (4-5) ml比1+am2x2+.+0mXn=0 若记 1 12 n 七 L21 A= a2 A2n Ami Xn

第四章 线性方程组 设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 21 1 22 2 2 11 1 12 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     若记 （4-5） 一、齐次线性方程组解的性质 11 12 1 1 21 22 2 2 1 2 , n n m m mn n a a a x a a a x A x a a a x             = =            

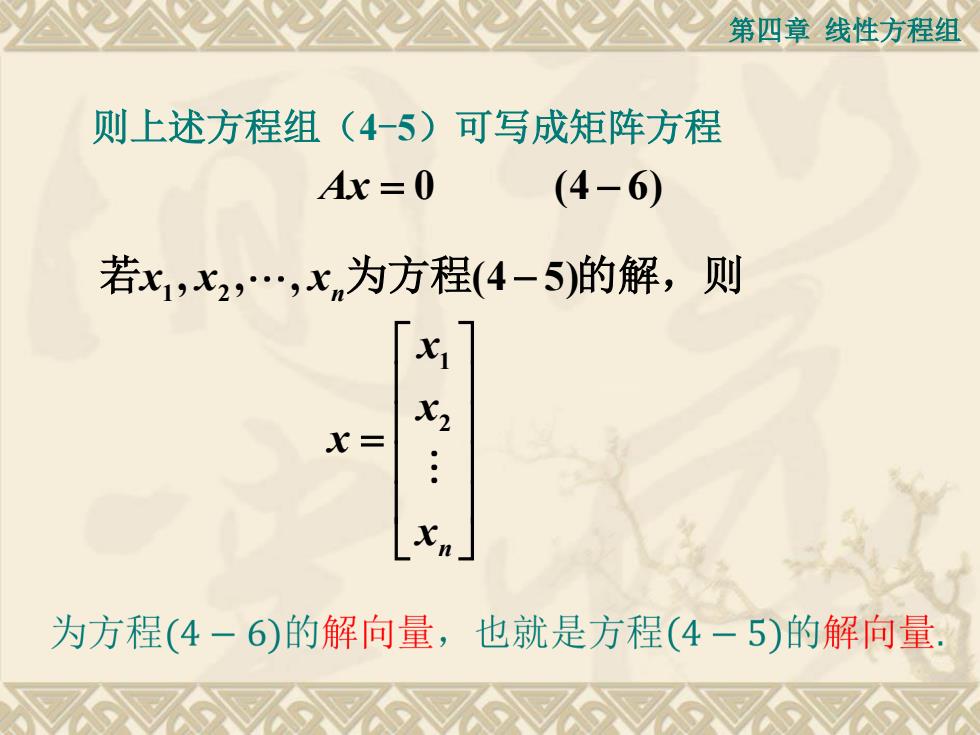
第四章线性方程组 则上述方程组(4-5)可写成矩阵方程 Ax=0 (4-6) 若x1,x2,.,xn为方程(4-5)的解，则 X2 X= Xn 为方程(4-6)的解向量，也就是方程(4-5)的解向量

第四章 线性方程组 则上述方程组（4-5）可写成矩阵方程 Ax = − 0 (4 6) 1 2 1 2 , , , (4 5) n n x x x x x x x −       =       若 为方程 的解，则

第四章线性方程组 性质4.2.1两个解向量的和仍然是解向量，即 设5,5，是方程组(4-5)的解向量，则5+5也 是方程组(4-5)的解向量. 证明只需证明5+52满足方程组(4-6)即可 因为A5=0,A52=0, 所以A(5+52)=A51+A52=0, 故x=51+52也是Ax=0的解

第四章 线性方程组 1 2 1 2 , (4 5 4.2. ) (4 5 1 )     − + − 两个解向量的和仍然是解向量，即 设 是方程组 的解向量， 性质 则 也 是方程组 的解向量. 证明 所以A A A (    1 2 1 2 + = + = ) 0， 1 2 因为A A   = = 0, 0， 故 x 也是Ax 0的解. =  1 +  2 = 只需证明  1 2 + 满足方程组(4 6) − 即可

第四章线性方程组 性质4.2.2一个解向量的倍数仍是解向量，即 设ξ是方程组(4-5)的解向量，几是任意数， 则2ξ也是方程组(4-5)的解向量. 证明由于A(25)=九A(5)=九0=0. 所以5也是方程组(4-5)的解向量

第四章 线性方程组 (4 5) (4 5 . .2 ) 4 2     − − 一个解向量的倍数仍是解向量，即 设 是方程组 的解向量， 是任意数， 则 性质 也是方程组 的解向量. 证明 由于A A (    ) = = = ( ) 0 0. 所以 也是方程组(4 5) − 的解向量