《线性代数》课程教学课件（讲稿，B）第四章 线性方程组 §4.1 线性方程组的解的判别

第四章线性方程组 Ch4 线性方程组 ●§4.1线性方程组的解的判别 。§4.2齐次线性方程组的解的结构 ● §4.3非齐次线性方程组解的结构

第四章 线性方程组 Ch4 线性方程组 §4.2 齐次线性方程组的解的结构 §4.1 线性方程组的解的判别 §4.3 非齐次线性方程组解的结构

第四章线性方程组 §4.1线性方程组的解的判别 >一、引例 。二、线性方程组的解的判别方法

第四章 线性方程组 §4.1 线性方程组的解的判别 一、引例 二、线性方程组的解的判别方法

第四章线性方程组 、引例 n元线性方程组 01七1+412X2+.+41mXn=b1 a21X1+022X2+.+02mxn=b2 (4-1) mX1+m2大2++0mmXn=bnm 记 41 l12 1n 11 412 . ain A= L21 a22 ,A= 21 022 Ami Am2 Ami Am2

第四章 线性方程组 n 元线性方程组 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (4 1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =  −    + + + = 11 12 1 11 12 1 1 21 22 2 21 22 2 2 1 2 1 2 , n n n n m m mn m m mn m a a a a a a b a a a a a a b A A a a a a a a b             = =             记 一、引例

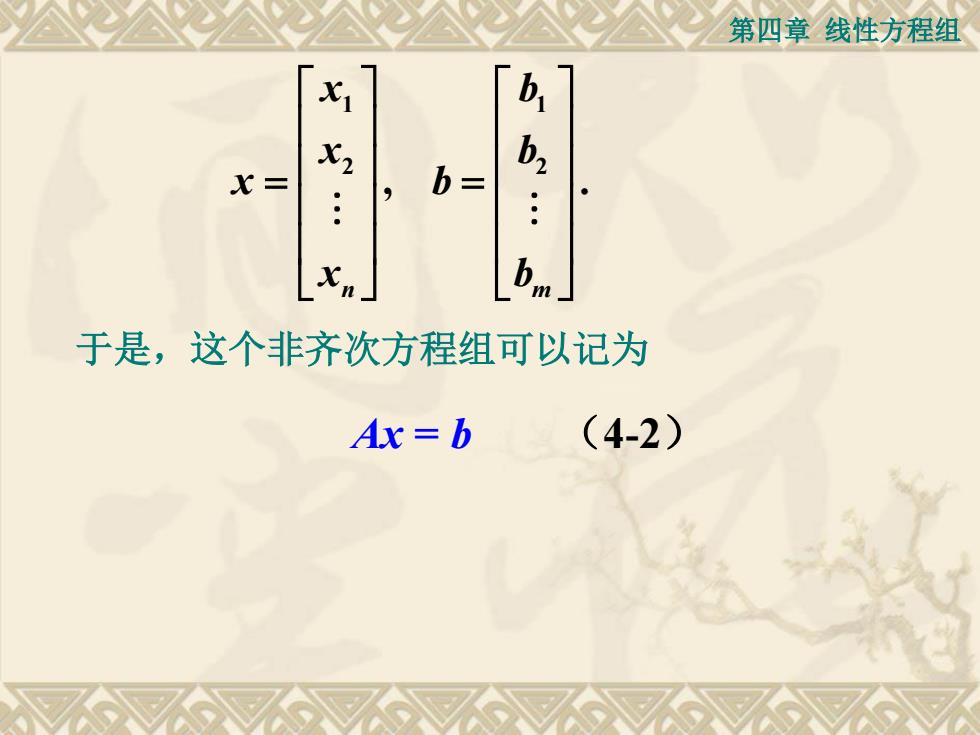
第四章线性方程组 b x= ·. ,b= Xn b 于是，这个非齐次方程组可以记为 Ax=b (4-2)

第四章 线性方程组 1 1 2 2 , . n m x b x b x b x b             = =             Ax = b （4-2） 于是，这个非齐次方程组可以记为

第四章线性方程组 由第二章的讨论可知，方程组(4-1)与增广矩阵 具有一一对应关系，对方程组进行加减消元相当 于对其增广矩阵进行初等变换，因此求解方程组 的问题就可以转化为矩阵的初等行变化问题. 一 般线性方程组的解可能会出现三种情况： 有唯一解、有无穷多解或无解

第四章 线性方程组 由第二章的讨论可知，方程组(4-1)与增广矩阵 具有一一对应关系，对方程组进行加减消元相当 于对其增广矩阵进行初等变换，因此求解方程组 的问题就可以转化为矩阵的初等行变化问题. 一般线性方程组的解可能会出现三种情况： 有唯一解、有无穷多解或无解