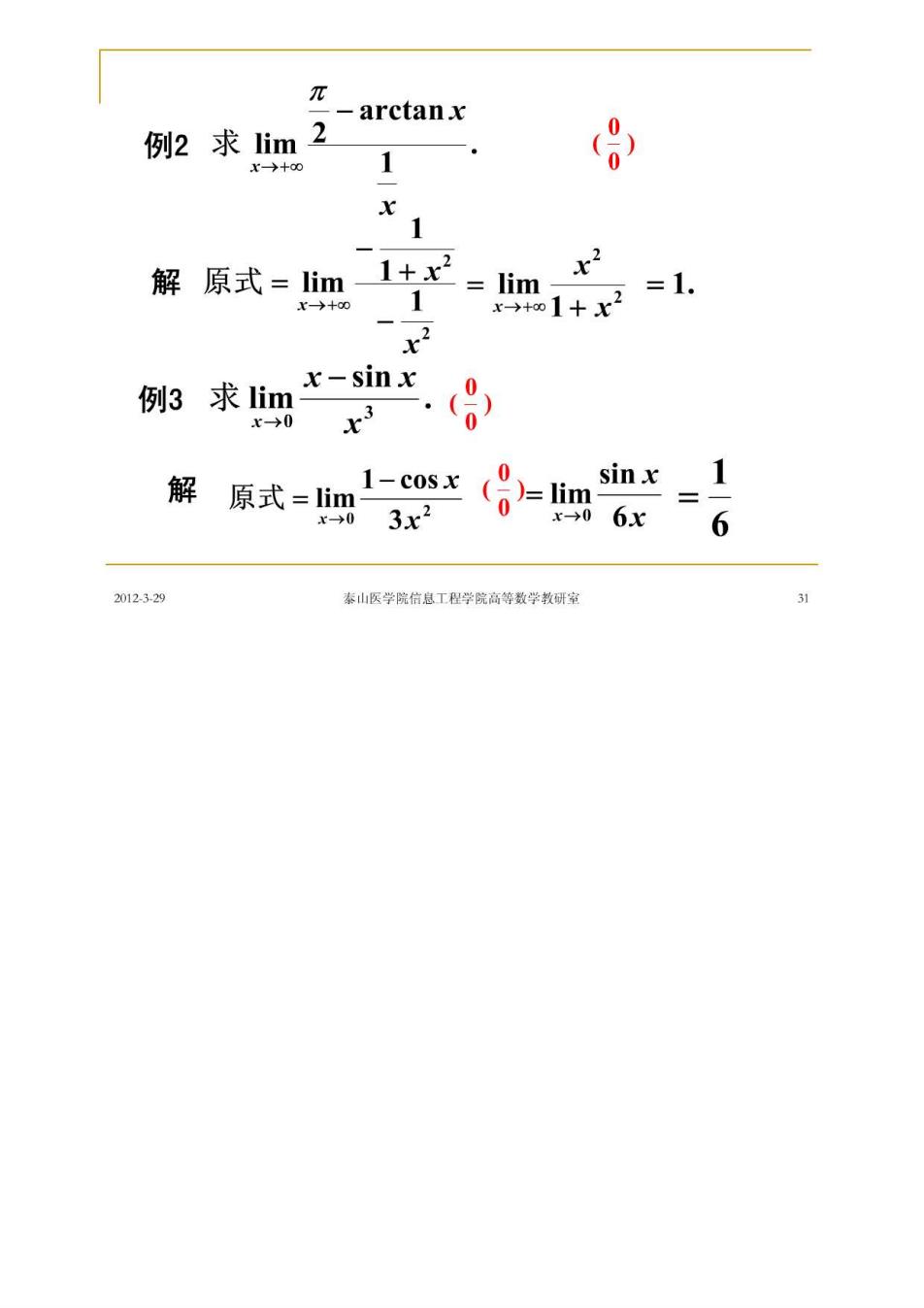
π -arctanx 例2求im2 3r)+00 1 解原式=lim 1+x2 -lim. 例3求lim x-sinx r-0 解 1-cosx(6x 原式=1im3x2 sinx 1 →0 =6 2012329 泰山医学院行息工程学院高等数学教研室

注意: 1)使用罗必塔法则必须验证条件,不是 未定式不能用罗必塔法则; 2)罗必塔法则可以连续应用,必须步步化 简(尽可能地化简)、步步验证求未定式 的极限. tanx-x 例4 lim x→0x2sinx 原式=lim tanx-x x-→0x2.x ,=1im secx-1 →03x2 lim (tanx)=lin x21 03x203x2=3 2012329 泰山医学院信息工程学院高等数学教研室 52

定理2() 00 设(1)当x→a时,函数f(x)及F(x)都趋于无穷: (2)在a点的某邻域内(点a本身可以除外),f'(x) 及F'(x)都存在且F'(x)≠0; 6)imf四存在(或为无穷大 Fx) 郑米四得四得 f'(x) 当x→∞时,该法则仍然成立. 2012329 泰山医学院信息工程学院高等数学教研室

例5 求lim tanx xtan3x 解原式=lim sec2x =lim cos23x 3sec23x 3 c0sx 1lim-6cos3xsin 3x 3x2 -2cosxsinx =lim Sin6.x →sin2x =lim 6cos6x =3. 2c0s2* 2012329 泰山医学院佑息工程学院高等数学教研室

注意3:若导数比的极限不存在,不能判断 原函数极限不存在。 例如,lim七-sinx 1-cosx lim x→ox+sinx x→o1+c0sx 1-sin 事实上lim x=1 1+sin ex-ex=lim ex-ex lim e*+e r→∞ex+ex ea+e号me lim e'(-e") =1 m(1+e25 2012329 素山医学院信息工程学院高等数学教研室