
目录》 01 常系数线性常微分方程 CONTENTS 02 常系数线性偏微分方程
目 录 CONTENTS 01 常系数线性常微分方程 02 常系数线性偏微分方程
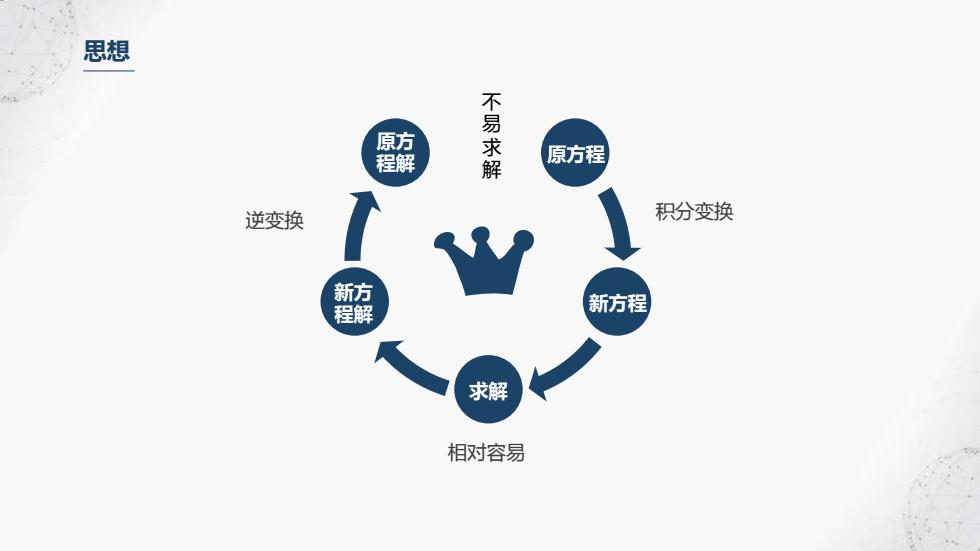
思想 原方 程解 不易求解 原方程 逆变换 积分变换 新 解 新方程 求解 相对容易
思想 逆变换 积分变换 相对容易 原方 程解 原方程 新方程 新方 程解 求解 不 易 求 解

01 PART 常系数线性常微分方程
常系数线性常微分方程 01 PART

例题 例1求微分方程x"(t)-3x'(t)+2x(t)=e3t满足x(0)=x'(0)=0的 解. 解设L[x(t)]=X(s),由导数性质,得[x'(t)]=sX(s)-x(O)=sX(s), L[x"(t)]=sL[x'(t)]-x'(O)=s2X(s).方程两边做Laplace变换,得 (s2-3s+2)X0时=_1 S-3 从而Xs)=s-6-2s-·对X()做Laplace逆变换得到 1 0-0-e+ 经检验该解适合原方程
例题 例1 求微分方程 𝑥 ′′ 𝑡 − 3𝑥′ 𝑡 + 2𝑥 𝑡 = 𝑒 3𝑡 满足 𝑥 0 = 𝑥 ′ 0 = 0 的 解. 解 设 L 𝑥(𝑡) = 𝑋(𝑠),由导数性质,得 L 𝑥′(𝑡) = 𝑠𝑋 𝑠 − 𝑥 0 = 𝑠𝑋(𝑠), L 𝑥′′(𝑡) = 𝑠L 𝑥′(𝑡) − 𝑥′ 0 = 𝑠 2𝑋(𝑠).方程两边做 Laplace 变换,得 𝑠 2 − 3𝑠 + 2 𝑋 𝑠 = 1 𝑠 − 3 , 从而 𝑋 𝑠 = 1 (𝑠−1)(𝑠−2)(𝑠−3).对 𝑋 𝑠 做 Laplace 逆变换得到 𝑥 𝑡 = 1 2 𝑒 𝑡 − 𝑒 2𝑡 + 1 2 𝑒 3𝑡. 经检验该解适合原方程.

例题 例2求微分方程组 x'(t)=-x(t)+y(t)+et y'(0=-3x()+2y(0+2et 满足x(0)=y(0)= 1的解. 解设[x(t)〗=X(s),Ly(t)]=Y(s),由导数性质,得[x'(t)】= sX(s)-x(0)=sX(s)-1,[y(t)]=sY(s)-y(0)=sY(s)-1.方程 两边做Laplace变换,得 6+1)X(s)-Y(s)=。s S-1 3X(s)+(s-2)Y(s)= s+1 s-1 解得Xs)=Y(s)=一·对Xs),Ys)做Laplace逆变换得到x(d= y)一et.经检验该解适合原方程组
例题 例2 求微分方程组 ൝ 𝑥 ′ (𝑡) = −𝑥 𝑡 + 𝑦 𝑡 + 𝑒 𝑡 𝑦 ′ (𝑡) = −3𝑥 𝑡 + 2𝑦 𝑡 + 2𝑒𝑡 满足 𝑥 0 = 𝑦 0 = 1 的解. 解 设 L 𝑥(𝑡) = 𝑋(𝑠),L 𝑦(𝑡) = 𝑌(𝑠),由导数性质,得 L 𝑥′(𝑡) = 𝑠𝑋 𝑠 − 𝑥 0 = 𝑠𝑋 𝑠 − 1,L 𝑦′(𝑡) = 𝑠𝑌 𝑠 − 𝑦 0 = 𝑠𝑌 𝑠 − 1.方程 两边做 Laplace 变换,得 𝑠 + 1 𝑋 𝑠 − 𝑌 𝑠 = 𝑠 𝑠 − 1 , 3𝑋 𝑠 + 𝑠 − 2 𝑌 𝑠 = 𝑠 + 1 𝑠 − 1 . 解得 𝑋 𝑠 = 𝑌 𝑠 = 1 𝑠−1 .对 𝑋 𝑠 ,𝑌(𝑠) 做 Laplace 逆变换得到 𝑥 𝑡 = 𝑦 𝑡 = 𝑒 𝑡.经检验该解适合原方程组.