
Chapter 6 Jointly Distributed Random Variables
Chapter 6 Jointly Distributed Random Variables

6.1 Joint distribution functions For any two random variables X and Y.the joint cumulative probability distribution function of X and Y by F(a,b)=P(X≤a,Y≤b)-o<a,b<o
6.1 Joint distribution functions var , (,) ( , ) , joint cumulative probability distribution For any two random iables X and Y f the u of X and Y by F ab P X aY b nct a b ion = ≤ ≤ −∞< <∞
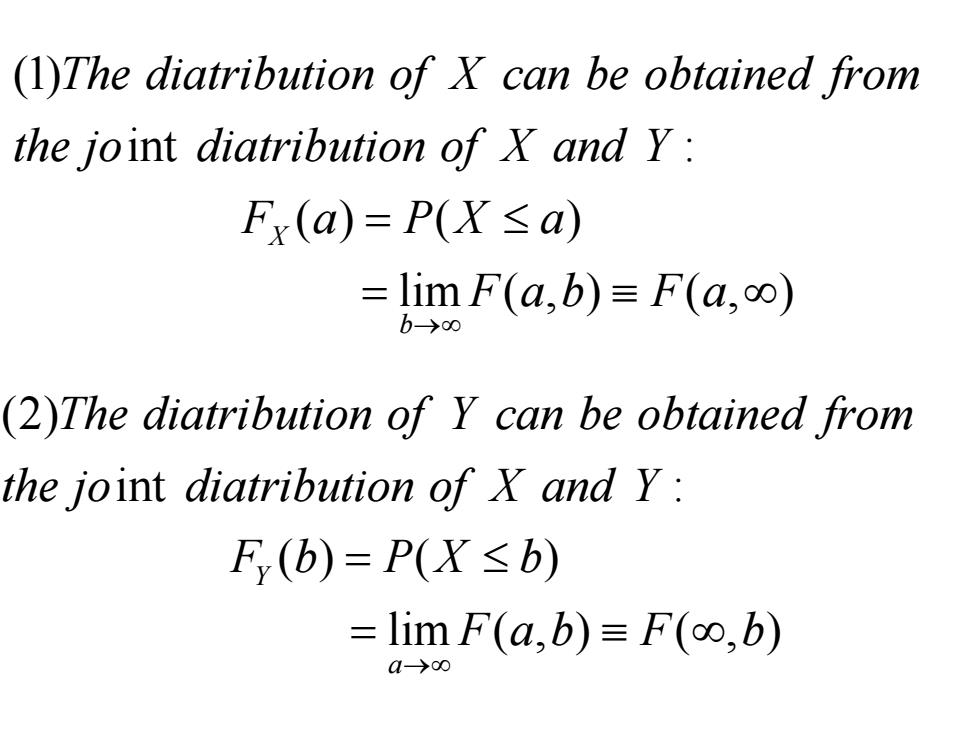
(1)The diatribution of X can be obtained from the joint diatribution of X and y: Fx(a)=P(X≤a) =limF(a,b)≡F(a,oo) b→00 (2)The diatribution of Y can be obtained from the joint diatribution of X and Y: F,(b)=P(X≤b) =limF(a,b)≡F(oo,b) a-→00
(1) int : () ( ) lim ( , ) ( , ) X b The diatribution of X can be obtained from the jo diatribution of X and Y F a PX a F ab F a →∞ = ≤ = ≡∞ (2) int : () ( ) lim ( , ) ( , ) Y a The diatribution of Y can be obtained from the jo diatribution of X and Y F b PX b F ab F b →∞ = ≤ = ≡∞

Notice P(a1<X≤a2,b<Y≤b) =F(a2,b2)+F(a,b)-F(a,b)-F(a2,b) Whennever a <a,b<b2
1 21 2 2 2 11 12 21 1 21 2 ( ,) (,) (,) (,) (,) , . Pa X a b Y b Fa b Fab Fab Fa b Whennever a a b b < ≤ <≤ = +−− < < Notice

Discrete random variables Define the joint probability mass function of X and Y by p(x,y)=P(X=x,Y=y) The probability mass function of X can be obtained from p(x,y)by px(x)=P(X=x) =∑p(x,y) y:p(x,y)>0
Discrete random variables (, ) { , } Define the joint probabi of X and Y by pxy lity mass functio PX x y n = = = Y :(,)0 ( , ) () { } (, ) X yp xy The probability mass function of X can be obtained from p x y by p x PX x pxy > = = = ∑