
x3-3x+2 0 -2-x+1 例1求lim 型 0 解:原式=lim 3x2-3 x13x2-2x-1 6x ,3 li 、 x16x-22 注意:不是未定式不能用洛必达法则! 6x 6 li x-16x-2 ≠lim6=l x→>16 2009年7月3日星期五 6 目录○ 上页 下 返回
2009年7月3日星期五 6 目录 上页 下页 返回 . 1 23 lim 23 3 1 − − + +− → xxx xx x 解: 原式 lim →1 = x 0 0 型 26 6 lim 1 − = → x x x 2 3 = 注意: 不是未定式不能用洛必达法则 ! 26 6 lim →1 x − x x 1 6 6 lim 1 = x→ ≠ 33 2 x − 123 2 xx −− 例1 求
例2求lim 3-6 arctan x 型 0 X>+00 1 1 解:原式=lim 1+x X>十0∞ 1 00 2 型 00 x2 1 lim lim X+01+x2 =I >+∞21 思考:如何求lim 号-arctann (n为正整数)? n-→o0 1 n 2009年7月3日星期五 7 目录 上页 、返回
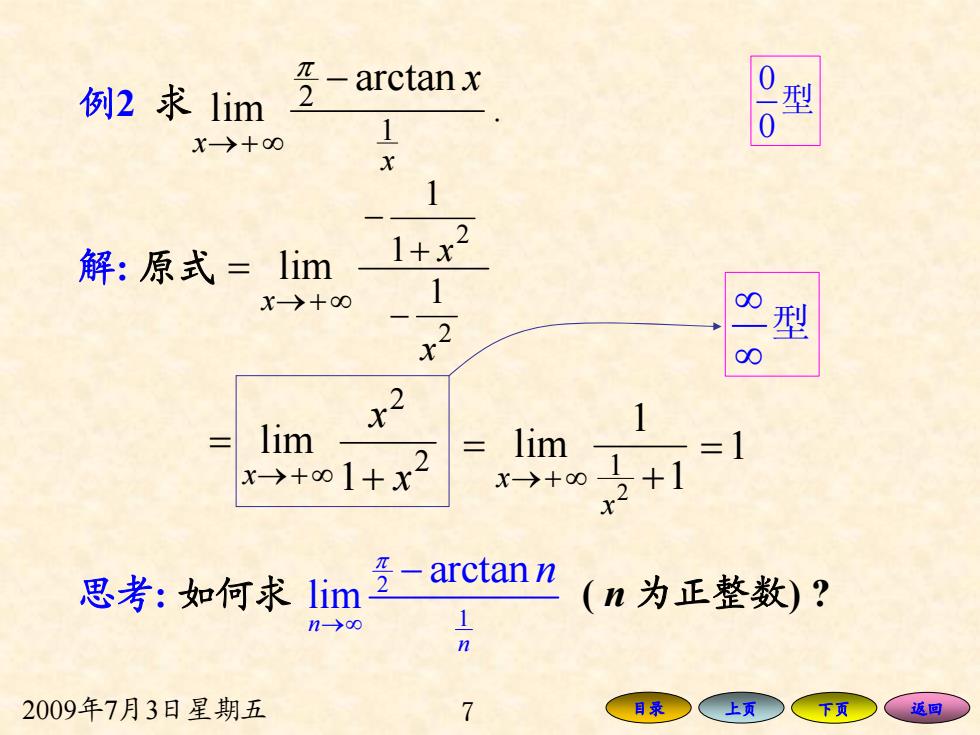
2009年7月3日星期五 7 目录 上页 下页 返回 . arctan lim 1 2 x x − x ∞+→ π 解: 原式 lim ∞+→ = x 0 0 型 2 2 1 lim x x x + = ∞+→ =1 2 1 1 + x − 2 1 x − 1 1 lim 2 1 + = ∞+→ x x 思考: 如何求 2 1 arctan limn n n π →∞ − ( n 为正整数) ? ∞ ∞ 型 例2 求

二、”型未定式的洛必达法则 00 定理2. 1)limf(x)=limF(x)=o X→a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)1im四存在(或为) x→aF'(x) lim '(x) (洛必达法则) x→aF(x) xa F(x) (证明略) 2009年7月3日星期五 8 日录 上页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 二、 型未定式的洛必达法则 ∞ ∞ 1) lim ( ) lim ( ) xa xa f x Fx → → = = ∞ )( )( lim)3 xFf x ax ′′ → 存在 (或为∞) ( ) lim ( ) x a f x → F x 定理 2. (证明略) ( ) lim ( ) x a f x → F x ′ = ′ (洛必达法则) 在与 axFxf 内可导,)()()()2 D ∪ 且F′ x ≠ 0)(

说明:定理中x→a换为 x→a, X→a,x→0, x→十0, X〉-0 之一,条件2)作相应的修改,定理仍然成立 2009年7月3日星期五 9 目录 上页( 下顶 返回
2009年7月3日星期五 9 目录 上页 下页 返回 说明: 定理中 → ax 换为 之一, 条件 2) 作相应的修改 , 定理仍然成立. , → + ax , → − ax x → ∞, x +∞→ , x −∞→