
第一章 第五节极限运算法则 (Techniques for Finding Limits 一、数列极限的四则运算 二、函数极限的四则运算法则 三、无穷小量的运算法则 四、复合函数的极限运算法则 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 第五节 极限运算法则 第一章 (Techniques for Finding Limits ) 二、函数极限的四则运算法则 一、数列极限的四则运算 三、无穷小量的运算法则 四、复合函数的极限运算法则

一、数列极限的四则运算 定理1若lim=A,lim yn=B,则有 n->oo n->oo (I)lim(xn±yn)=A±B (2)lim xnyn AB n-→o0 (3)当y,≠0且B≠0时,1imn=4 n-→∞ynB 注意:定理1中的(1)、(2)可推广到有限个收敛 数列的情形.例如,如果limx=A,limy=B,lim2n=C, n→0 n->oo 1n→o 则有lim(xn+yn-2n)=limx+lim y-limzn=A+B-C n-→00 n→0 lim()=limx,lim ylim=A.B.C n>0 n-→0 n-→0 2009年7月3日星期五 2 目录 上页 下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、数列极限的四则运算 yAx n B ,lim,lim n n n = = → ∞ → ∞ 则有 )(lim)1( nn n ± yx → ∞ nn n yx → ∞ lim)2( ≠ By ≠ 时且当 ,00)3( n B A y x n n n = ∞→ lim = A ± B = A B 定理1 若 注意: 定理 1中的( 1)、( 2)可推广到有限个收敛 数列的情形 . 例如, lim , lim ,lim n nn nn n xA yB zC →∞ →∞ →∞ 如果 = = = , 则有 lim ( n nn ) n xyz →∞ + − lim lim lim n nn nnn xyz →∞ →∞ →∞ = + − = A + B C− lim( ) n nn n xyz →∞ lim lim lim n nn nn n xyz →∞ →∞ →∞ = ⋅ ⋅ = A⋅ B C⋅

1 2 例1 lim 2十 3 ?(习题1-51(3)) n-→o n n n(n+1) 解:原式=lim2 =lim(1+) n->oo n-→02 1 =lim.lim(1+-) n→02n→0 n 1 .(lim1+lim 2`n→0 n-→on 2009年7月3日星期五 3 目录○ 、上页○ (下页 、返回
2009年7月3日星期五 3 目录 上页 下页 返回 ? 321 lim 222 2 =⎥⎦ ⎤ ++++ ⎢⎣ ⎡ ∞→ n n n nnn " 解 : 原式 2 1 ( 1) 2 limn n n →∞ n + = ) 1 1( 2 1 lim n n += ∞→ 例 1 1 1 lim lim(1 ) n n →∞ →∞ 2 n =⋅+ 1 1 (lim1 lim ) 2 n n →∞ →∞ n =⋅ + 1 (1 0) 2 =⋅+ 1 2 = (习题1-5 1 ( 3))

二、函数极限的四则运算法则 定理2若limf(x)=A,limg(x)=B (1)lim[f(x)+g(x)]=4+B (2) lim[f(x)-g(x】=A-B. (3) lim[f(x)g(x)]=AB. (4) lim f()4 (B≠0) 8(x)B 说明:定理2中的(1)、(2)可推广到有限个函数相 乘的情形. 推论1lim[Cf(x)]=Clim f(x) (C为常数) 推论2lim[f(x)]”=[limf(x)]” (n为正整数) 2009年7月3日星期五 4 目录 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 二、函数极限的四则运算法则 定理2 若 (1) lim[ ( ) ( )] . f x gx A B − = − lim[ ( ) ( )] . (2) (3) f x g x AB = (4) lim ( ) ,lim ( ) f x A gx B = = lim[ ( ) ( )] . f x gx A B + = + ( ) lim . 0 ( ) fx A B gx B = ( ) ≠ 说明: 定理 2中的( 1)、( 2)可推广到有限个函数相 乘的情形 . 推论 1 C f = Cx f x)(lim)](lim[ ( C 为常数 ) 推论 2 n n = xfxf ])(lim[)](lim[ ( n 为正整数 )
三、无穷小量的运算法则 定理3有限个无穷小的代数和仍是无穷小 思考: 1 lim 解答见课本第六节例3 说明:无限个无穷小之和不一定是无穷小! 2009年7月3日星期五 5 目录 上页 下页 、返回
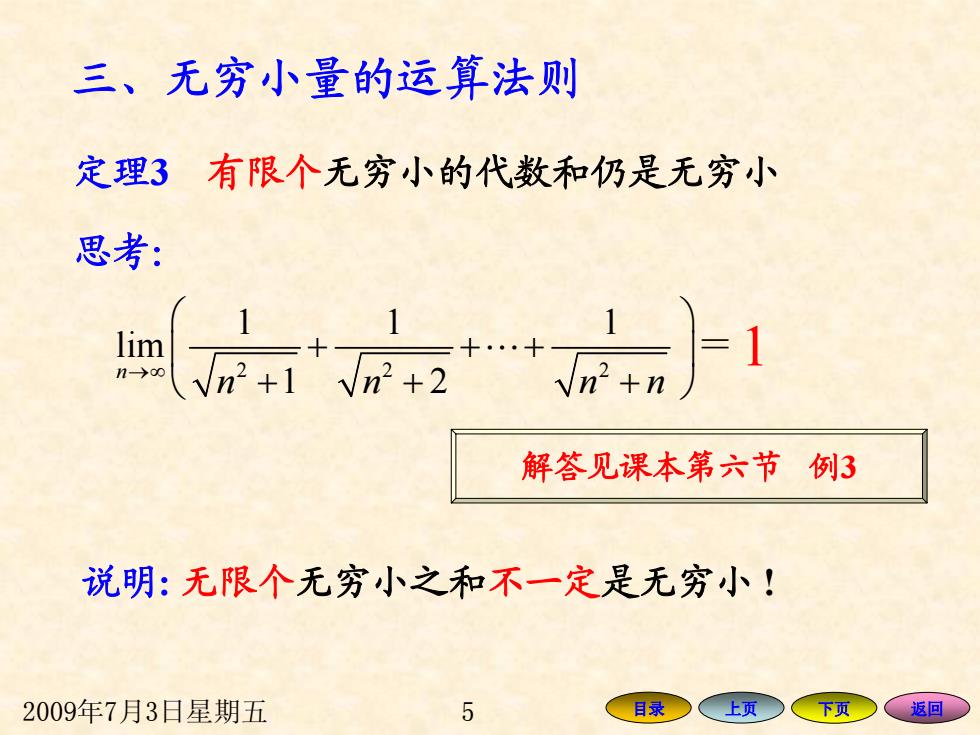
2009年7月3日星期五 5 目录 上页 下页 返回 三、无穷小量的运算法则 定理3 有限个无穷小的代数和仍是无穷小 思考: 22 2 11 1 lim 1 2 n n n nn →∞ ⎛ ⎞ ⎜ ⎟ + ++ ⎝ ⎠ ++ + " =?1 解答见课本第六节 例 3 说明 : 无限个无穷小之和不一定是无穷小 !