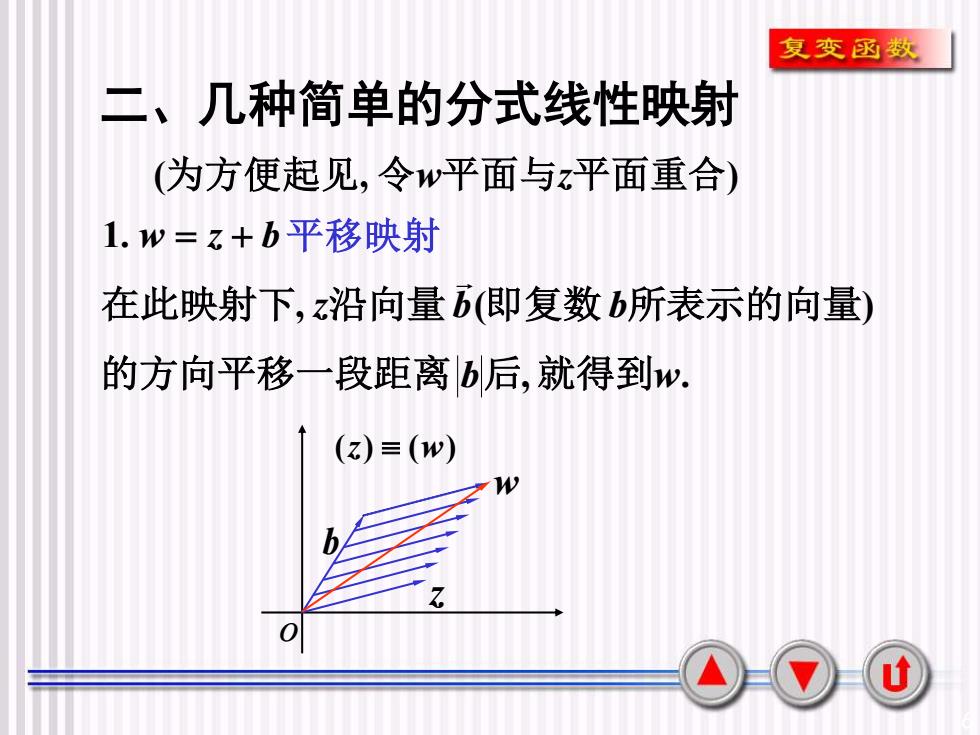
复变函数二、几种简单的分式线性映射(为方便起见,令w平面与z平面重合)1.w=z+b平移映射在此映射下,z沿向量b(即复数b所表示的向量)的方向平移一段距离b后.就得到W(z) = (w)W110u
6 o (z) (w) z b w 二、几种简单的分式线性映射 1. w = z + b 平移映射 (为方便起见, 令w平面与z平面重合) 在此映射下, z沿向量b(即复数b所表示的向量) 的方向平移一段距离 b后,就得到w
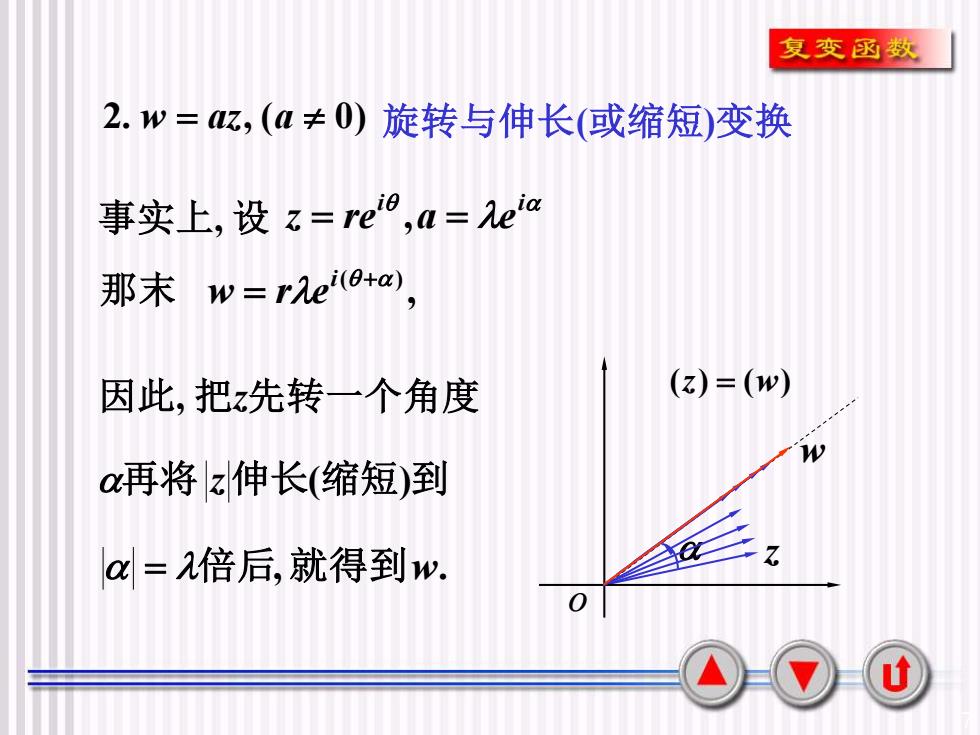
复变函数2. w=az,(a ≠ O)旋转与伸长(或缩短)变换事实上,设z=reio,a=Meiα那末 W=rei(0+α)(z) = (w)因此,把先转一个角度Wα再将z伸长(缩短)到aMα=a倍后,就得到w.0u
7 2. w = az, (a 0) 旋转与伸长(或缩短)变换 事实上, 设 i i z = re ,a = e 那末 , ( ) + = i w r e 因此, 把z先转一个角度 再将 z伸长(缩短)到 = 倍后,就得到w. w z o (z) = (w)

复变函数3. W =反演变换Z此映射可进一步分解为W=WW=7欲由点作出点W,可考虑如下作图次序Z关于横轴对称关键:在几何上如何由z一→w,?u
8 关于横轴对称 z w 1 3. = 反演变换 此映射可进一步分解为 , 1 1 z w = w = w1 欲由点z作出点w, 可考虑如下作图次序: z → z → w1 → w 关键: 在几何上如何由z → w1 ?

复变函数对称点的定义:设C为以原点为中心.r为半径的圆周.在以圆心为起点的一条半直线上,如果有两点P与P满足关系式OP.Op'=r2,那末就称这两点为关于这圆周的对称点规定:无穷远点的对称点是圆心0.u
9 对称点的定义: 设C为以原点为中心, r为半径的圆周. 在以 圆心为起点的一条半直线上,如果有两点P与P 满足关系式 , 2 OP OP = r 那末就称这两点为关于这圆周的对称点. 规定: 无穷远点的对称点是圆心O
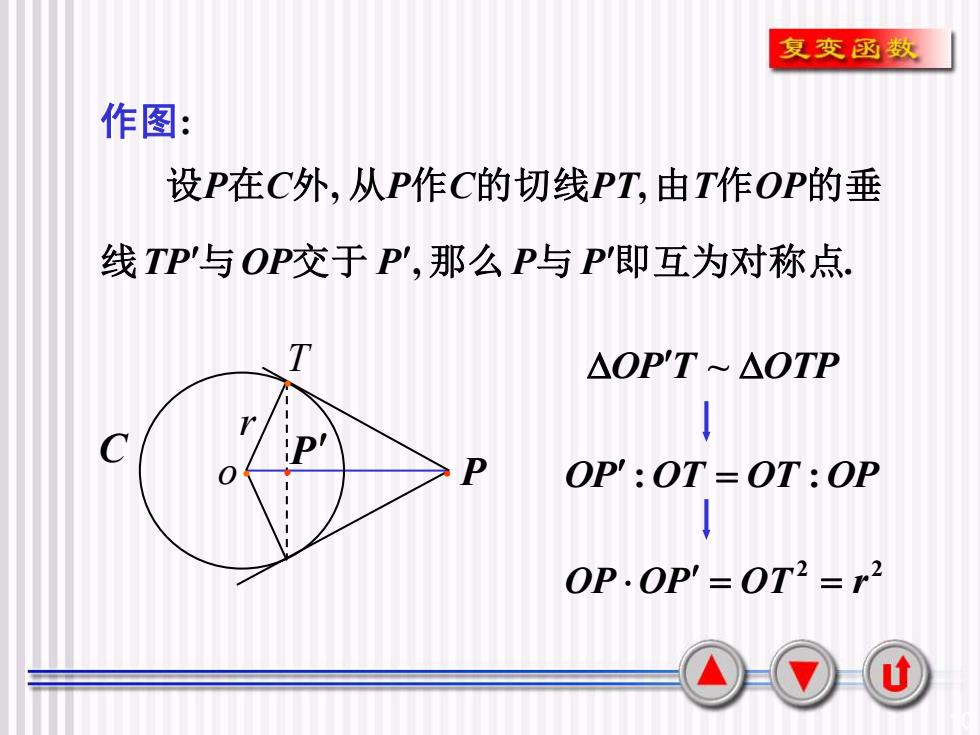
复变函数作图:设P在C外,从P作C的切线PT.由T作OP的垂线TP'与OP交于 P',那么P与 P'即互为对称点TAOP'T ~△OTPCiP'POP:OT = OT : OPO---OP:OP= OT2 = r2u
10 r C o. . P P . 设P在C外, 从P作C的切线PT, 由T作OP的垂 线TP与OP交于 P , 那么P与 P即互为对称点. OPT ~ OTP OP :OT = OT :OP 2 2 OP OP = OT = r 作图: T