
第一章 第三节函数的极限 (Limits of Functions) 在前一节我们讨论了数列的极限,本节主要介 绍一般函数的极限以及其性质, 一、函数极限的定义 二、函数极限的性质 2009年7月3日星期五 目录○ 上页 下页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第三节 函数的极限 (Limits of Functions) 第一章 在前一节我们讨论了数列的极限,本节主要介 绍一般函数的极限以及其性质 . 二、函数极限的性质 一、函数极限的定义

一、函数极限的定义 如果函数f(x)在自变量的某个变化过程中,对应的函数值 无限接近于某个确定的数A,那么这个确定的数A就叫做在这 一变化过程中函数的极限. 由于自变量的变化过程不同,函数的极限就表现为不同 的形式: 数列极限可看作函数f(n)当n→o时的极限,这里自变 量的变化过程是n→o(n∈W).注意:这里的n是离散变化的. 下面主要研究当自变量x趋于无穷大或趋于有限值时, 函数f(x)的极限.注意:这里的x是连续变化的. 2009年7月3日星期五 2 目录 上页 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、函数极限的定义 如果函数 f x( ) 在自变量的某个变化过程中, 对应的函数值 无限接近于某个确定的数 A , 那么这个确定的数 A 就叫做在这 一变化过程中函数的极限. 由于自变量的变化过程不同,函数的极限就表现为不同 的形式. 数列极限可看作函数 f ( ) n 当 n → ∞ 时的极限, 这里自变 量的变化过程是n nN →∞ ∈ ( ). 下面主要研究当自变量 x 趋于无穷大或趋于有限值时, 函数 f ( ) x 的极限. 注意:这里的 n 是离散变化的. 注意:这里的 x 是连续变化的.
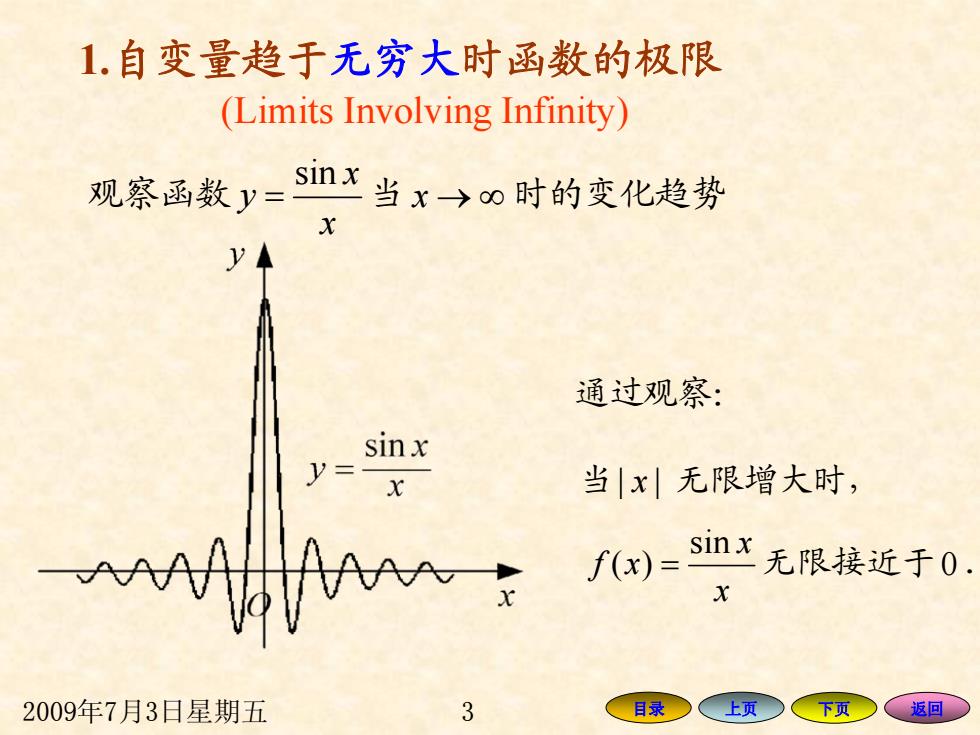
1.自变量趋于无穷大时函数的极限 (Limits Involving Infinity) 观察函数y=sinx当x→∞时的变化趋势 通过观察: sinx 当|x无限增大时, ,fm)=snx无限接近于0. 2009年7月3日星期五 3 目录 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 观察函数 sin x y x = 当 x → ∞ 时的变化趋势 1.自变量趋于无穷大时函数的极限 (Limits Involving Infinity) 通过观察: 当| | x 无限增大时, sin ( ) x f x x = 无限接近于 0 .

问题:如何用数学语言刻画函数“无限接近”? 我们用f(x)-A<ε表示f(x)-A任意小;用|x>X 表示x趋于无穷大的过程 定义1设函数f(x)当|x|大于某一正数时有定义.如果 存在常数A,对于任意给定的正数ε(无论它多么小),总存在 正数X,使得适合不等式x>X的一切x所对应的函数值f(x) 都满足不等式 f(x)-A<8, 那么常数A就叫做函数f(x)当x趋于无穷大时的极限,记作 limf(x)=A或f(x)>A(x→o). 2009年7月3日星期五 4 目录 上页 下页 、返回
2009年7月3日星期五 4 目录 上页 下页 返回 问题: 如何用数学语言刻画函数 “无限接近 ” ? 我们用 fx A ( ) − < ε 表示 f ( ) x A − 任意小; 用| | x X > 表示 x 趋于无穷大的过程. 定义 1 设函数 f ( ) x 当| | x 大于某一正数时有定义. 如果 存在常数 A ,对于任意给定的正数 ε (无论它多么小), 总存在 正数 X , 使得适合不等式| | x X > 的一切 x 所对应的函数值 f ( ) x 都满足不等式 fx A ( ) − < ε , 那么常数 A 就叫做函数 f ( ) x 当 x 趋于无穷大时的极限, 记作 lim ( ) x f x A → ∞ = 或 f ( ) x A → ( x → ∞ ).
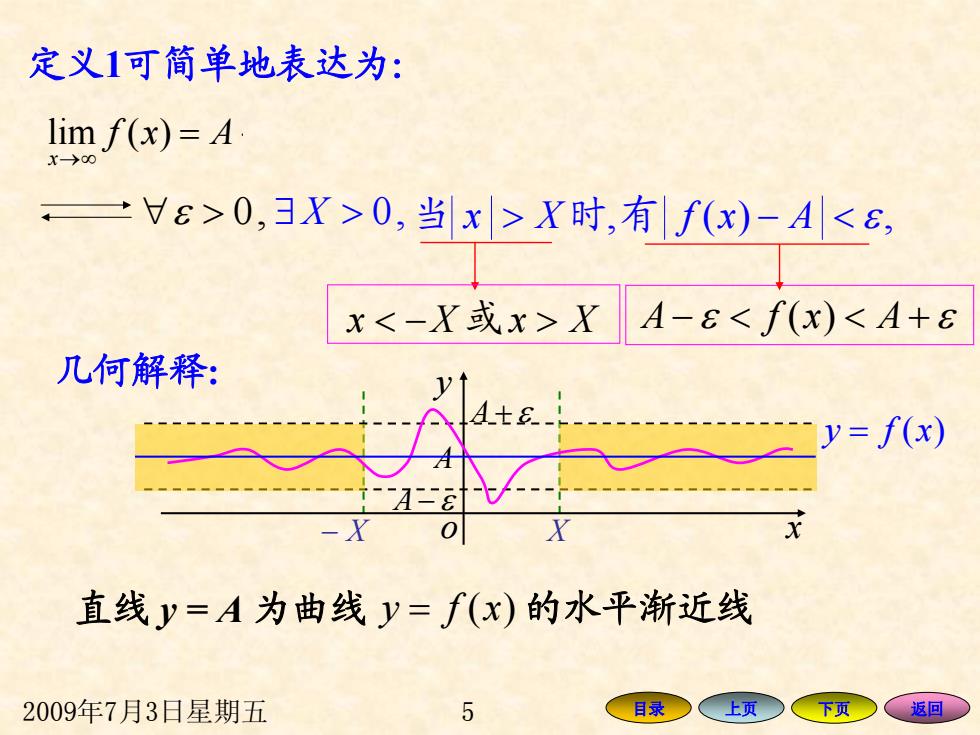
定义1可简单地表达为: lim f(x)=4 X->00 =廿6>0,3X>0,当x>X时,有f(x)-A<6, x<-X或x>XA-E<f(x)<A+ε 几何解释: y=f(x) 直线y=A为曲线y=f(x)的水平渐近线 2009年7月3日星期五 5 目录 上页 下页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 定义 1可简单地表达为: lim ( ) x f x A →∞ = ⇔ ∃ X > ,0 当 > 有时 − AxfXx < ε ,)(, < − 或 > XxXx A − ε < f x)( < A + ε ∀ ε > ,0 − X X A + ε A − ε o x y y = f ( x ) A 几何解释 : 补充定义 如果li m ( ) x f x A →∞ = , 那么直线 y A = 是函数 y f = ( ) x 的图形的水平渐进线. 直线 y = A 为曲线 y = f ( x ) 的水平渐近线