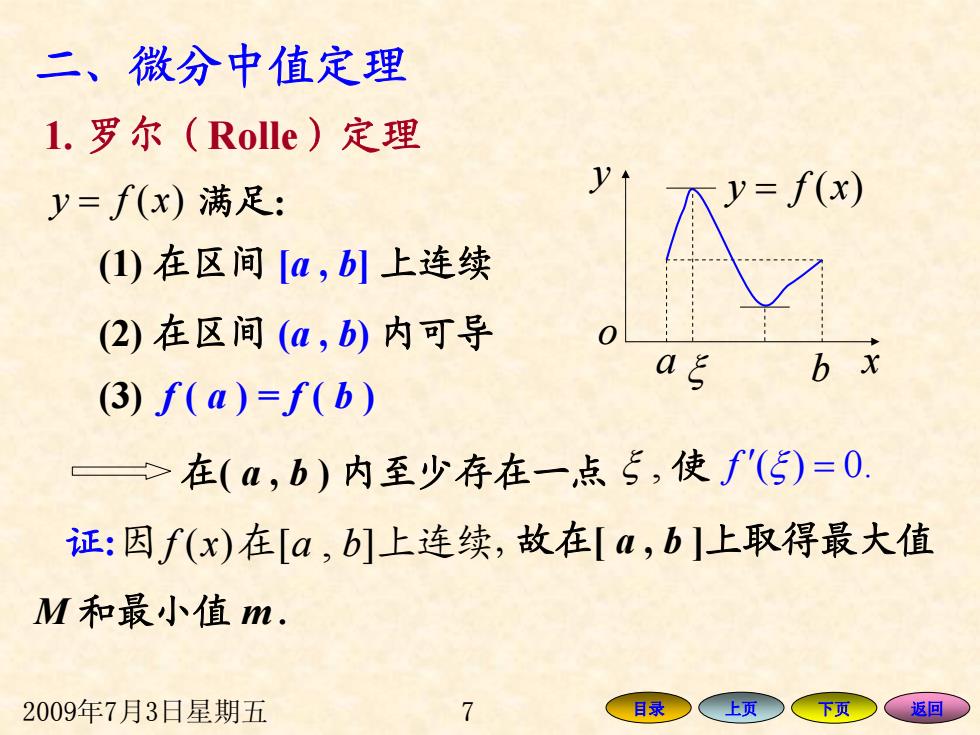
二、微分中值定理 1.罗尔(Rolle)定理 y=(x)满足: =f(x) (I)在区间[a,b]上连续 (2)在区间(a,b)内可导 (3)f(u)=f(b) →在(a,b)内至少存在一,点5,使'(5)=0. 证:因f(x)在[a,b]上连续,故在[a,b]上取得最大值 M和最小值m. 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 二、微分中值定理 1. 罗尔(Rolle)定理 y = f x)( 满足 : (1) 在区间 [ a , b ] 上连续 (2) 在区间 ( a , b ) 内可导 (3) f ( a ) = f ( b ) ξ , 使 f ′( ) 0. ξ = x y o a b = xfy )( ξ 证 : 因 在 baxf ],[)( 上连续,故在[ a , b ]上取得最大值 M 和最小值 m . 在( a , b ) 内至少存在一点

若M=m,则f(x)≡M,x∈[a,b],因此V5∈(a,b), f'(5)=0. 若M>m,则M和m中至少有一个与端,点值不等, 不妨设M≠f(a),则至少存在一点5∈(a,b),使 f(5)=M,则由费马引理得f'(5)=0. 注意:定理条件条件不全具备,结论不一定成立 例如, a- 2009年7月3日星期五 8 目录 上页 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 若 M = m , 则 f x ≡ M ∈ bax ,],[,)( 因此 ∀ ξ ∈( , ), a b f ′( ) 0. ξ = 若 M > m , 则 M 和 m 中至少有一个与端点值不等 , 不妨设 M ≠ f a ,)( 则至少存在一点 ξ ∈ ba ,),( 使 f ξ = M ,)( 则由费马引理得 f ′( ) 0. ξ = 注意 : 定理条件条件不全具备, 结论不一定成立. 例如 , ⎩ ⎨ ⎧ = ≤ < = 1,0 10, )( x xx xf 1 x y o

f(x)=x f(x)=x x∈[-1,1] x∈[0,1] 例1设f(x)在[0,1]上连续,在(0,1)内可导,且f(1)=0, 证明至少存在一点5∈(0,1),使 5f'(5)+f(5)=0. 提示:5f'(5)+f(5)=(f(x)川- 2009年7月3日星期五 0 目录 上页 (下页 、返回
2009年7月3日星期五 9 目录 上页 下页 返回 ]1,0[ )( ∈ = x f xx ]1,1[ )( −∈ = x f xx 1 x y − 1 o 1 x y o 例 1 设 f ( ) x 在[0,1]上连续, 在(0,1) 内可导, 且 f (1) 0, = 证明至少存在一点 ξ ∈ (0,1), 使 ξ f f ′( ) ( ) 0. ξ ξ + = 提示: ( ) ( ) ( ( )) x f f xf x ξ ξξ ξ = ′ ′ + =