
第二节数列的极限 12 n 3 2 一般项 n n+1 Xn= n+1 2,4,.,2” 一般项xn=2”, 1 1 1 24 一般项 2 1,-1,.,(-1)1,. 一般项xn=(-1)+1, 1 n+(1,一般项 x,= n+(-1)r- 上页 下页 返回 MathGS 公式 线与面 数学家
第二节 数列的极限 , , 1 , , 3 2 , 2 1 n + n 一般项 , +1 = n n xn 2 , 4 , , 2 , , n 一般项 2 , n n x = , , 2 1 , , 4 1 , 2 1 n 一般项 , 2 1 n n x = 1, 1, , ( 1) , , − − n+1 一般项 ( 1) , +1 = − n n x , , ( 1) , , 2 1 2 , 1 n n n− + − 一般项 . ( 1) 1 n n x n n − + − =

第二节数列的极限 对于数列,我们要研究的问题是: 当→o时,数列{xn}是否能无限接近于某个确 定的常数?如果能,如何求这个常数? 上页 下页 返回 MathGS 公式 线与面 数学家
第二节 数列的极限 对于数列,我们要研究的问题是: 当 n→ 时,数列 { xn } 是否能无限接近于某个确 定的常数? 如果能,如何求这个常数?
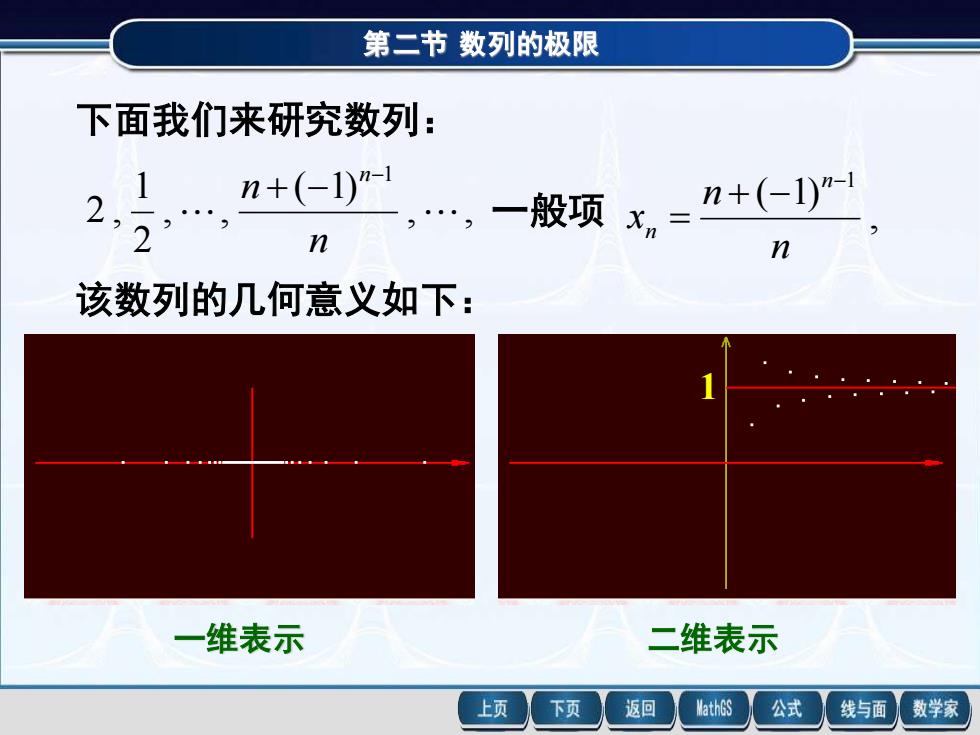
第二节数列的极限 下面我们来研究数列: 1 2 n+(-1)"-1 n+(-1)"- 2 n 一般项x,= n 该数列的几何意义如下: 一维表示 二维表示 上页 下页 返回 MathGS 公式 线与面 数学家
第二节 数列的极限 下面我们来研究数列: , , ( 1) , , 2 1 2 , 1 n n n− + − 一般项 , ( 1) 1 n n x n n − + − = 该数列的几何意义如下: 一维表示 二维表示 1